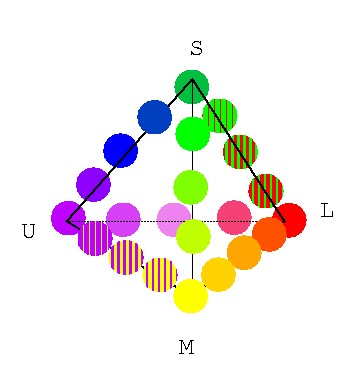
図 4-6 4原色色空間の各辺の色を表わした図.(再掲)
さて4次元の場合(6)の復習. まず4原色の色空間である正四面体(図 4-6)を 膨らませて,色球(図 4-11)を作ろうとした. しかし球面上での座標と言うのは案外わかりにくい. そこで正六面体にしたものが図 4-14, 4-15, 4-16, 4-17 というわけだ.実際には正六面体の各面の中央を少し飛びださせると (面の形が三角形の24面体になる)より球に近づくだろう.
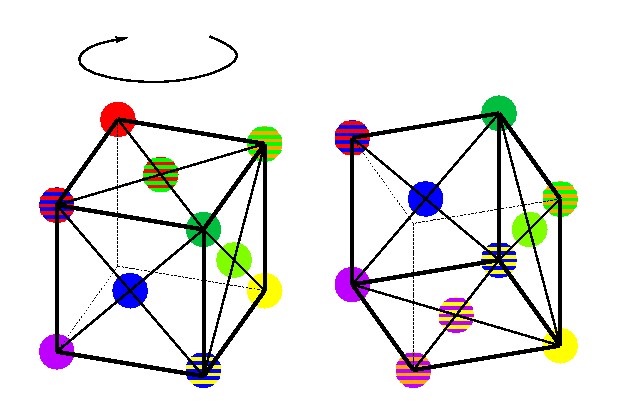
斜め上から見たところと,斜め下から見上げたところ.
以下,90度ずつ回転していく.
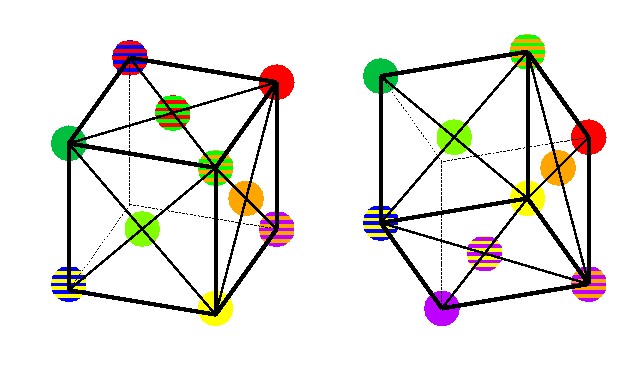
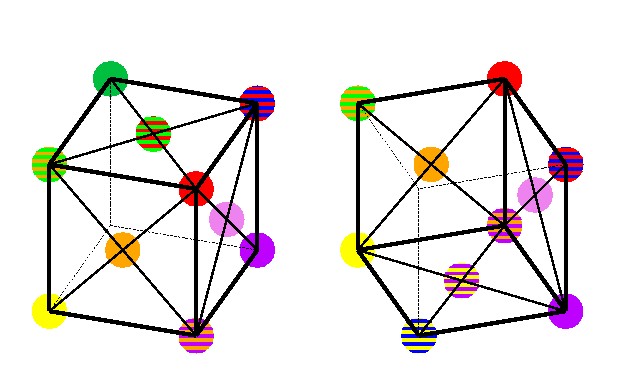
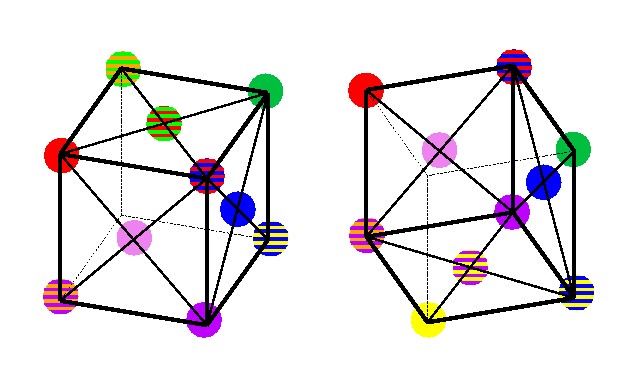
図 4-14, 4-15, 4-16, 4-17 立方体で表現した色球.左右のペアはそれぞれ斜め上/下から見たもの.各段は90度ずつ回転させた時の図を示している.(再掲)
球に近づけようとする理由は2つある.一つは,色と色との相互関係を理解する時, 正四面体では頂点や辺がいわば特別な点になってしまいやすい.完全に球になって しまえば,原色は互いに対等な関係になり,正四面体と言う形に捕われることなく 色と色との相互関係を理解しやすくなるということだ.
もう一つの理由は座標のとり方だ.3原色の場合,元々は (l, m, s ) と いう3次元ベクトルで表現されていた光を,明度・色相・彩度という3つの 心理物理量の形に座標変換していた.そして 色相と彩度は,3原色色空間に おける極座標表示として理解できる.すなわち中央の無彩色を原点として, 原点からの距離を彩度,原点からの方角を色相として捉えるのだ.
では4次元空間の場合,いったいどのような心理物理量に座標変換されるの だろうか.もう一度光応答空間の次元数と対応させて復習してみよう.
1次元 → 明度という具合だ(※注.2原色の場合,彩度が存在しないという考え方はおそらく 正しくない.ただしここでは4次元の色について考えることを本題とするため, 話を単純化して,とりあえず上記のように書いておく).
2次元 → 明度・色相
3次元 → 明度・色相・彩度
では4原色の場合,色を表現するのに色相と彩度以外に新たな「何か」が 導入されるのだろうか? われわれ3原色生物には感じられない,新しい色の 属性が発生するのだろうか.この疑問について考えるためには,色球上にどのように 色が配置されるかを考える必要があった.その結果として,そこそこ球に近く, かつ互いの位置関係もわかりやすい「色立方体」にたどりついた.
上記の疑問に対して,現時点での私の考えはNOだ. すなわち色相や彩度以外の新しい属性は発生しないと思う. それは色立方体上の色の配置を見ればわかる. どうも4原色生物は,ひとつの色に対して同時に2つの色 (←われわれが感じるところの)の属性を与えることができるようだ. 例えば赤緑とか黄紫という具合に.そして,ひとつの属性の強度を固定したまま, もう一つの属性を変えることができる.たとえば黄紫→黄青→黄緑というように.
ということは,色相を表現するに二つの次元が必要だと言うことになる. 4原色生物でも,色を原点を中心とした3次元空間の極座標で表わすことは 可能だろう.そして原点(無彩色)からの距離が彩度となるのも同じだ. しかし残りの二つの角度は,どちらも色相を表わすと考えられる.
このことは,色球上で単波長光が複雑な軌跡を描くことともつながる. すくなくとも色球上で単波長光のみを他の色と区別するような簡単な 座標変換は存在しない(3原色空間では彩度という軸を使って分離できた). おそらく4原色生物は,単波長光と,他の原色とを特別に区別していないのでは ないか(われわれもまた,赤紫を他の単波長光と特別に区別していないと言える. ただ,われわれの場合,原色のメンバーで単波長光に属さないのが赤紫のみで, それ以外はすべて単波長光で表現可能な色である).
先の掲示で「明度・色相・彩度に次ぐ第4の属性はないのではないか. むしろ色相が2次元になるのではないか」と書いた.これは十分な (説得力のある)根拠の元に言っているのではなく,現時点での推測に過ぎない. 4原色の色空間をいろいろ探検して見た感触として述べているだけなのだが, 第4の属性になりそうなものは(今のところ)見つかっていないし, その一方で色相を2次元と考えることで色空間におけるの連続的な変化を 理解しやすいように思う.もっともこれだけでは納得させるのに不十分な 説明だとは自分でも感じているが.このあたり,意見を聞かせてもらえたらうれしい.
さて長々と掲示してきたが,最後に「4原色で物を見ている生物はいるのか」という 話をして締めくくりたい.
以前にも述べたように,4種の錐体を持つ生物は実際にいて,キンギョ(とその 類縁)を例として挙げた.ただしこの場合は反対色チャネルが2種しかなく, 4原色の色空間を持っているとは考えられないということも述べた.4原色の 色空間は正四面体という3次元の立体で表わされ,そのうちの1点を座標として 指し示すためには,3つの一次独立な座標軸が必要になる.すなわち反対色 チャネルが3つ必要になる.
反対色チャネルを3つ持つ生物としては魚のウグイが知られている. ウグイの2次ニューロンの波長特性をおおざっぱに示したものが図 4-20 だ.
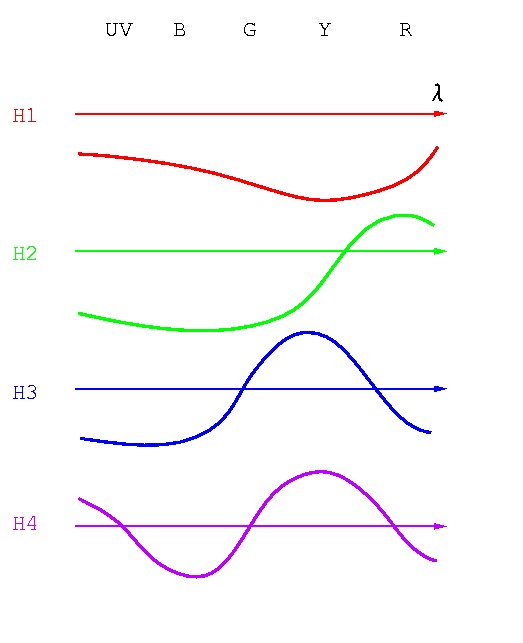
図 4-20 ウグイの2次ニューロン(水平細胞)の波長応答特性
ウグイはH1, H2, H3, H4の4種の錐体入力性二次ニューロン(水平細胞)を持つ (この他に桿体入力性のがある).実はH1, H2, H3まではコイやキンギョも 持っており,H4がウグイで見つかったものだ.
このうちH1はすべての波長の光に対してマイナスの応答を示す.つまり H1は明るさ情報に対応すると考えられる.それに対してH2はUV・青・緑vs赤の 反対色を示す.これを4原色の色空間で示すとこうなる(図 4-21).
H2は正四面体を垂直に2分する2つの領域に分けることがわかるだろう.
H3はUV・青・赤vs黄の反対色を示す.これも同様に 4原色の色空間で示すとこうなる(図 4-22).
H3も正四面体を垂直に2分する2つの領域に分ける. H1, H2, H3までだとコイやキンギョの場合と同じだ.これだけだと 正四面体の水平方向の座標を示すことはできるが,垂直方向の座標を示すことが できない.
ではウグイのH4の場合はどうなるだろうか.H4について 4原色の色空間で示すとこうなる(図 4-23).
この場合,正四面体を斜めに2分する.3つの反対色チャネルは(直交こそしないが) 一次独立であり,3次元の色空間の座標を指定することができる.
以上のことから,少なくとも網膜の初期段階においてウグイは4原色として 色の情報処理をしていることがわかる.もちろん本当に4原色として感じているか どうかはより高次のニューロンを調べてみないとなんとも言えない (それについてはほとんど調べられてないだろう).
これで4原色の色空間の話は(私の方からは)ひとまず終わりと言うことにしたい. いずれ機会(と時間)があれば,まとまった話として読めるようにWeb上で 整理するつもりでいる.
コーヒーの飲み過ぎで明け方過ぎまで寝られず,布団の中でもんもんとしながら 考えるのは4次元色の話.すると,上で紹介した以外にもまだまだ切り口や 探検方法があることに気がついた.
まず最初にお断り(くどいかもしれないが).4次元色なんて,そもそも わかりっこないのだ.だからこの掲示をつらつら読んだり,あるいは図を 眺めたくらいではわかった気にすらならないと思う.結局,自分で手を 動かして図を描いて見てようやく「ははあ,こうなっているのかあ」と 少しはわかった気になれるというもの(それでもやっぱりわからないものは わからないが).だからここで紹介できるのは,「3次元までの基礎知識」と 「4次元の探検方法」だけなのだ. これをガイドブックがわりに,探検するのはあなた自身.
さて今回紹介する探検方法.
コンピュータでは通常,R, G, Bをそれぞれ256階調で表現することが多い. この場合,1ピクセルが表現しうる色は (r, g, b) というベクトル空間であり, それぞれ 0〜255 までの整数値を入れることができる.ではこれを思い切り 単純化して,0 と 1 の2階調の場合で考えてみよう.この場合でも (0,0,0) から (1,1,1) までの8色を表わすことができる(昔懐かしい パソコンがこうでしたナ).
まず3次元でやってみるとこうなる(図 4-24).
(0,0,0) と (1,1,1) がないが,両者は黒と白に対応する. 互いに隣り合う色同士でベクトルの成分を比較した場合,常に1つしか違わない ということだ.
では同じ話を4次元でするとこうなる(図 4-25).
この場合も,隣り合う色とベクトル成分を比較すると1つしか違わないことに注意. そしてそれぞれの色に4bitの2進数を割り当てることができる.
もし今までの議論で出て来た「赤青」とか「黄紫」とかの名前が気に入らない (あるいはわかりにくい)のであれば,すべての色名を 1101 や 1100 のような 2進数のコード名に置き換えて考えてみると理解しやすいかもしれない.
以上,探検方法のちょっとしたヒント.
さて,せっかく4次元の色球を作ったのだから,経度・緯度を書き込むことで すべての色をうまく極座標上に表現できないか挑戦してみよう.
正六面体を横から眺めると正六角形に見える.ちょうど直角の向きから眺める ことで座標を見つけてみよう.ここでは緑と橙緑のラインを北極に, 紫と橙紫のラインを南極として見てみることにする.
図 4-26a は色球を赤道側から見た図だ.
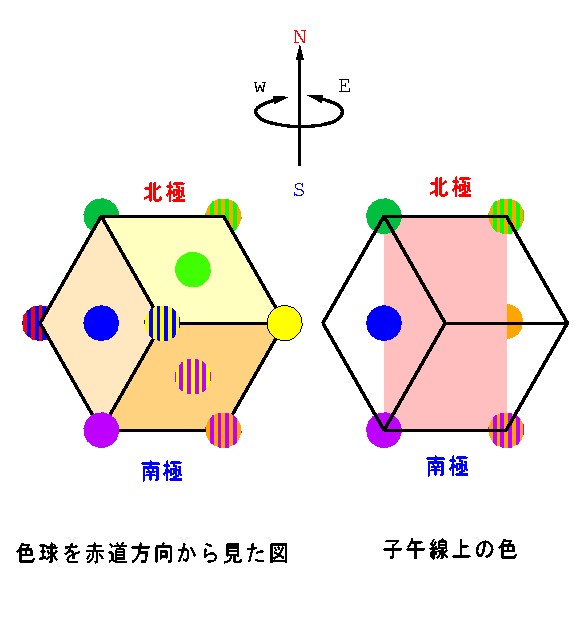
図 4-26a 緑−橙緑ラインを北極にした時の子午線上の色配置.
ここで北極と南極を通る子午線をひとつ決めて,その上に どんな色が並ぶか見てみよう.図 4-26aでは子午線が長方形になっているが, それは色球を立方体で表現したためで,実際には長辺(青と橙)が膨らんで 六角形になる.
次に図 4-26b は色球を北極側から見た図だ.
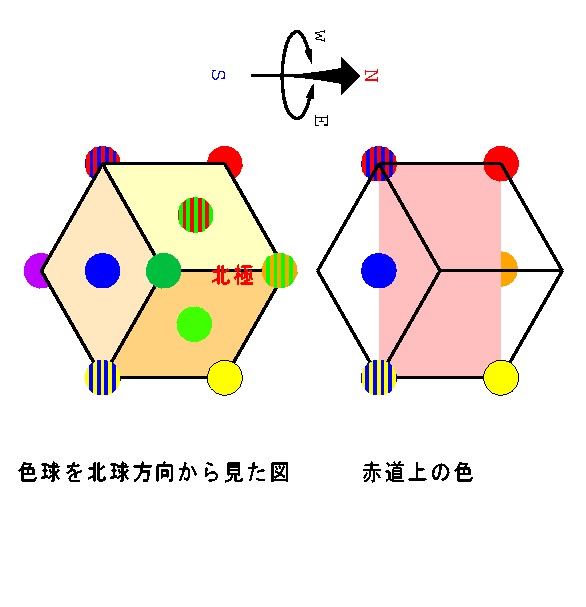
図 4-26b 緑−橙緑ラインを北極にした時の赤道上の色配置.
そして赤道上に位置する色を見てみよう.青と橙は 子午線と赤道が交わる点として選んだため,どちらの図(図 4-26a, b)にも出てくる.
子午線上の色と赤道上の色をピックアップしてみたのが図 4-27 だ.
図 4-26a, b では長方形の上に載っていた 6つの色を正六角形状に配置して見た(この方が色球に近くなる). 六角形の中央は色球の中心,すなわち無彩色で,対面する色同士は反対色に なっている.
図 4-27 をもう少し詳しく 見てみよう.上の段の子午線上の色に座標軸を取るなら,上下(南北)方向が 緑−紫軸,左右が青−橙軸と見ることができるだろう.同様に赤道上の色を 見ると,赤−黄軸と青−橙軸の2つを取ることができる.
子午線と赤道を組み合わせて再び立体に戻した図がこれだ(図 4-28).
色は3本の座標軸で位置を指定することができる. もっとも図 4-28 では何がなんだかわかりにくいので,同じ図を このように書き直して見た(図 4-29).
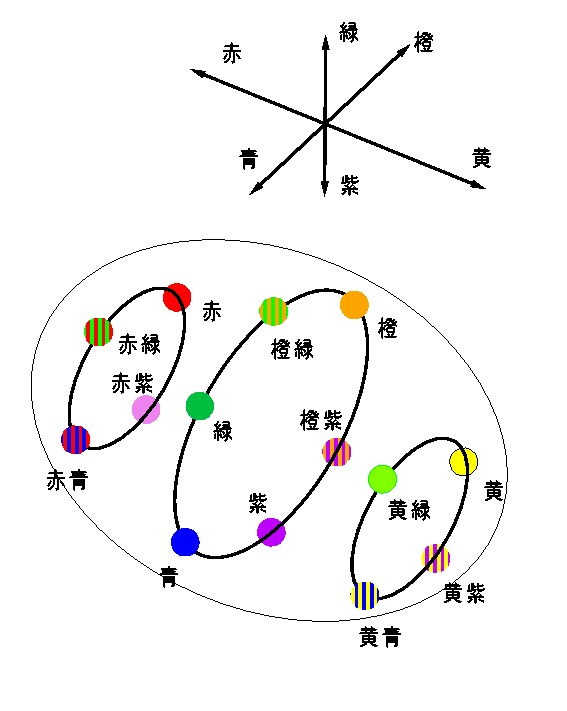
図 4-29 色球をタテに輪切りにしたときにできる3つの色環.
図 4-29 は,子午線と平行な円を描いた時に色球上でどんな風に色が変化するかを 表わしたものだ.3本の円形ラインの変化を見るとなかなか興味深い.
中央のラインというのが基本としてあって,それに対して
青 → 緑 → 橙 → 紫 → 青
赤よりのライン赤味を帯びた円と黄味を帯びた円ができる.
赤青 → 赤緑 → 赤 → 赤紫 → 赤青黄よりのライン
黄青 → 黄緑 → 黄 → 黄紫 → 黄青
同じように赤道と平行に一周して見たのが図 4-30 だ.
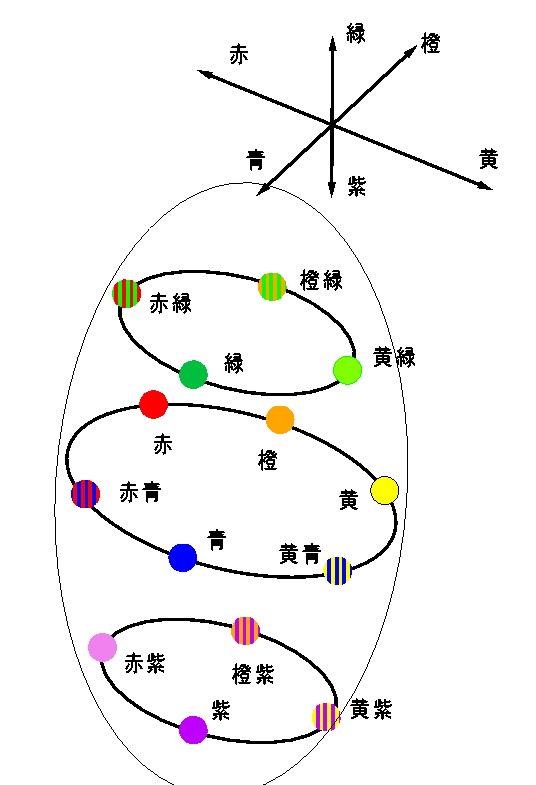
図 4-30 色球をヨコに輪切りにしたときにできる3つの色環.
図 4-30 でも赤道上の
青 → 赤 → 橙 → 黄 → 青という一周が基本としてあり,これが北極(緑)側に寄ると
緑 → 赤緑 → 橙緑 → 黄緑 → 緑という一周を描くし,逆に南極(紫)側に寄ると
紫 → 赤紫 → 橙紫 → 黄紫 → 紫という一周を描く.
これらのことを考えると,色球上の色は (r,θ,Φ) の3次元極座標で表現され, rが彩度,θとΦが共に(互いに直交し合う)色相を表わすと考えるのが 自然な気がするがどうだろう.
今まで4原色空間の色を色環ならぬ色球として表わすことを試みてきた. またなるべく正確な座標を示すため,球の代わりに正六面体(立方体)を 使って見た.座標の正確さを保ちながら,より球に近づけるには, 正六面体の頂点を切り落とした形 にすればいい.こうすることで立方体よりさらに球に近づき, 色同士の相対的な関係が見えてくる(図 4-31).
この方法を使ってさまざまな方角からみたのが図 4-32a だ.
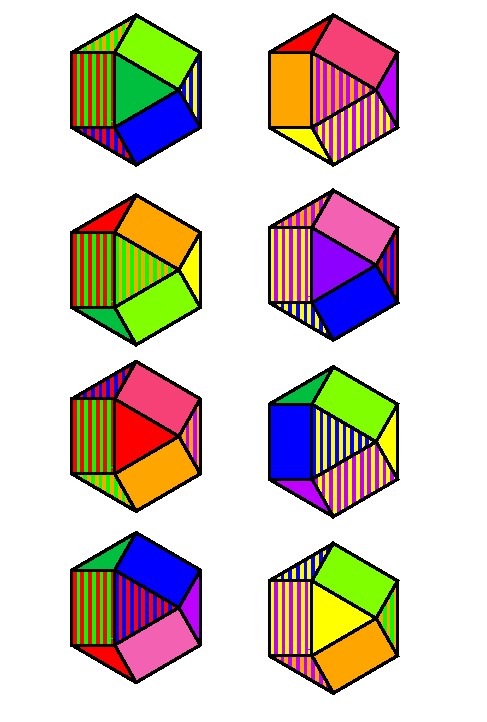
図 4-32a 14面体表現による色球をさまざまな角度から眺めたもの.左右のペアはちょうど反対側から見たものになる.
反対色ペアが左右に並ぶように配置したので,左右のペアはちょうど 正反対の側から眺めたものになる.
Prev: 4次元の場合 (b)
Next: 色の感じ方について
Top: 画像付き版の最初
[ テキスト版 ]
[ 色覚テキスト Top ]