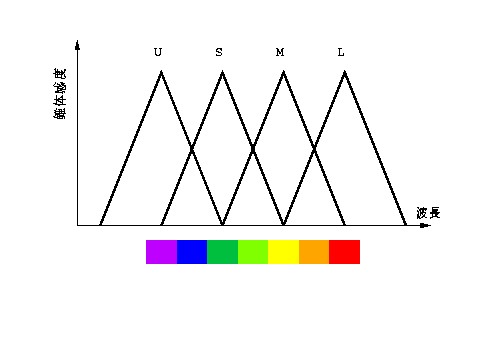
図 4-1 理想化した4種の錐体, U, S, M, L の波長感度特性
さていよいよ4次元の場合だ. 3次元のときとまったく同じやり方で,光応答空間を探検してみよう.
まず,錐体が4種ある.4種の名前を L, M, S, U としよう (U は Ultra Short の頭文字だ.あるいは Ultra Violet の頭文字でもいい). そしてこれらの波長特性をこの図のようにする (本当はUをUV領域に伸ばしたかったのだが,そうすると図が描けなくなるし, 私たち人間にとっても想像不可能になるので紫に対応させることにした).

図 4-1 理想化した4種の錐体, U, S, M, L の波長感度特性
これも今までと同じだ.そして光応答は (l, m, s, u ) という 4次元ベクトルとして表わされる.そこでこれまた今までと同様に, さまざまな強度,さまざまな波長の単波長光を与えた時に, (l, m, s, u ) 空間のどこにプロットされるかを見てみよう. 図 4-2 がその結果だ. (あいにく3次元空間に生きているわれわれにこの図を表現する有効な手段はない. 図に描けるはずがない!! ……のだが,無理して描いたのがこの図).
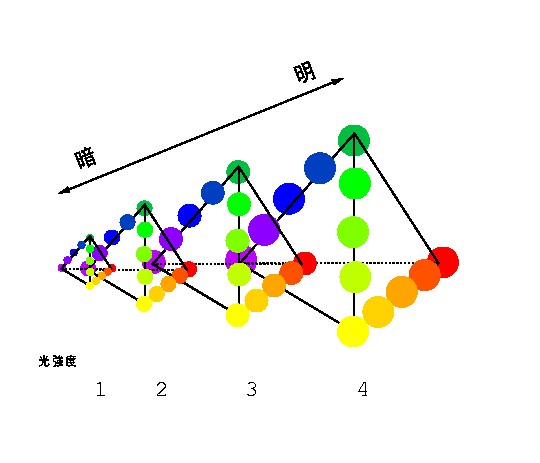
図 4-2 4次元の錐体応答空間(を無理矢理2次元上に描いたもの).単波長光の光強度を波長を変えた時の軌跡を描いている.
苦しい図を見てわかるとおり,(l, m, s, u ) 空間全体を描くのは無理だが, しかし光強度を一定にして波長のみを連続に変えた時に (l, m, s, u ) 空間内でどのような軌跡を描くかは表わすことができる.
2次元の場合,色空間は (0,1) と (1,0) をつなぐ1本の線分で表わされた. 光強度が1の光を,波長を連続的に変えながら与えると,光応答のベクトルはこの 線分上を移動した.同様に光強度2の光を与えた場合は,(0,2) と (2,0) をつなぐ 直線上を移動した.
3次元の場合,色空間は (0,0,1) と (0,1,0) と (1,0,0) をつなぐ正三角形上に 表わされた.
4次元の場合も同様だ.色空間は (0,0,0,1) と (0,0,1,0) と (0,1,0,0) と (1,0,0,0) をつなぐ3次元の立体として表わされる.この立体は頂点を4つ持ち, 各頂点間の距離はすべて等しい.つまり正四面体になる.
そこで光強度を1に固定したまま,波長だけを連続的に変えた場合の (l, m, s, u ) 上の軌跡,すなわち4次元の色空間を描いたものが 図 4-3 だ(先程の図 4-2 から光強度1の部分だけを取り出してきた).
すべての単波長光は,正四面体の辺LM, 辺MS, 辺SU の上に来る. 波長の短い順にたどってみよう.
U → S: 紫→青→緑光強度が2のときは,この正四面体の大きさが2倍になるだけだ. われわれの目的は,4原色生物がどう色を感じているかを知ることだ. 光強度が変わった時に明るさが変わって見えるという点では,4原色生物も 3原色生物も同じなので,今さら改めて考える必要はない.すなわち, この正四面体の中にどのような色が隠されているか,それを探検すれば よいということになる.
S → M: 緑→黄緑→黄
M → L: 黄→橙→赤
週末でいったんお休みしたけれど,4次元の続き. まず最初にお断りしておくけど,本来は赤・緑・青・UVを4原色に取るのが自然 なのだが,それだとディスプレイ上に色として表現できないし,「紫外線ってどんな 色に見えるんだ?」という,余計なことまで考えないといけない(4次元の色でさえ たいへんなのに,紫外線の色まで考えたくはない).そこで4原色を 紫(青紫)・緑・黄・赤として,考えている.この場合,これら4つの色を 頂点とする正四面体としてすべての色(明るさの成分は除く)が表わされるところまで 話をした.そこでこの正四面体上を探検しようという話が,前回までのあらすじ.
さて,この正四面体の上に単波長光をプロットすると 図 4-3 のように, 正四面体 USML の辺上に沿ってジグザグに並ぶことはすでに話した. これらはわれわれにとっても既知の色だ. では正四面体の他の部分にはどんな色が来るかを今回は考えてみる.
単波長光以外でわれわれが知っている色と言えば,赤紫系の色がある. これを書き加えてみよう.すると図 4-4 のように, 線分LU上に赤紫のラインができる.
これで青紫から始まって再び青紫で終わる色環ができたことになる. ただしこれがきれいなリングになるのは3原色の場合で,4原色の場合は 図 4-4 のようにV字に折れ曲がった二つの平面上に位置する変な形になっている.
われわれが知っているもう一つの色は(色と言ってよいかどうかわからないが), 白や灰色の無彩色がある.これは正四面体の中心に位置する. 中心が無彩色で,正四面体の表面に近づくほど色が鮮やかさを増す. すなわち正四面体中心を原点とした時,原点からの離れ具合が「彩度」を表わす という点においては,3原色も4原色も同じだ.正四面体の表面から中心へ向かって まっすぐ移動すると,色合い(色相)そのものは変わらないまま,どんどん色が 無彩色に近づいて行く.
これらのことから,以降は正四面体の表面だけを探検すればいいということに なる.内陸部については彩度を落としただけだから理解については困らないと言う わけだ.
4原色の色空間である正四面体に,われわれの知っている色を書き込む ところまで進んだ.いよいよこれから未知の色へと進むことになる.
まず考えて見たいのは,図 4-4 の線分UM上と線分LS上だ. 正四面体の辺の上でこれらの部分だけが空白のまま残っている.
未知の色は当然われわれの知っている色ではない.しかし
正四面体上でベクトルを連続的に動かした場合,感じる色も連続的に 変化するという原理を利用してそれらの色を想像してみよう.
まず線分UM上を考える.
線分UMの両端は紫と黄色だ.したがって点Uから徐々に点Mに向かってベクトルを 移動して行くと,紫から黄色に連続的に色が変化して感じるはずだ. さらに,中間地点の色は,紫と黄色の両方の特徴を持つ中間的な色に感じるはずだ. ちょうど赤紫が赤と紫の両方の特徴を持つ中間的な色として感じられるように. そこでこの場では,紫と黄色の中間の色を(便宜上)黄紫 と呼ぶことにする.
では黄紫という言葉を使って線分UM上をたどってみよう. すると次のように連続的に色が変わって感じるはずだ.
紫(スタート)これを強いて図で表現するなら,こんな感じになるだろう(図 4-5a).
↓
黄がかった紫
↓
紫味の強い黄紫
↓
黄紫
↓
黄味の強い黄紫
↓
紫がかった黄色
↓
黄色(ゴール)
「黄紫」という色がどんな色であるか,それだけではまったく想像することが できないが,このように前後の連続的な変化を考えることでどんな特徴を持った 色であるかは推測することができる.
ここで一つ注意すべき点がある.3原色で紫(青紫)と黄色は反対色の関係にある. したがって両者を混ぜると無彩色(灰色)になり,彩度が非常に低くなる. しかし4原色における「黄紫」という色は「赤紫」と同程度に鮮やかな色だ. 事実上,原色と思って良い.2原色生物にとって鮮やかな色をした「赤紫」が 想像できないのと同じように,3原色生物にとっては「黄紫」の色の鮮やかさや, ましてその美しさを想像することは不可能だ.
次に 正四面体の残った最後の辺, 線分SLを考えて見たい.線分SLは赤と緑を両端に持つ.したがってその中間の色は 赤緑 と名づけるのが適当だろう.
線分UMの場合と同様に,連続的な色の変化を考えてみよう.
緑(スタート)という具合だ.これを図にするならこんな感じになるだろう(図 4-5b).
↓
赤味がかった緑
↓
緑味の強い赤緑
↓
赤緑
↓
赤味の強い赤緑
↓
緑がかった赤
↓
赤(ゴール)
ここでも同じ話だが,4原色生物にとっての赤緑は鮮やかな原色の一員で あるということだ. 3原色生物の場合,赤と緑を混色するとただのグレーに近い彩度の低い色に なってしまうのだが.
「黄紫」や「赤緑」という色に対して,「名前をつけただけでちっともわかった 気がしない」という声があるかもしれない.もちろんそれはもっともな意見で, そもそも4原色の色なぞわかった気がする方がおかしい.しかし,だ. 「黄紫」だとか「赤緑」だとかいった色空間の一点のみを考えただけでは ちんぷんかんぷんでも,色の連続性から「緑味の強い赤緑」などの色を考えることで, このような未知の色が4原色色空間の上で矛盾なく存在し,しかも一定の特徴 (赤と緑の中間的な感じを持つなど)を有することはわかるはずだ.あとは各自想像を たくましくして少しでも感じ取ろうと努力する以外はないと思う.
正四面体の色空間の探検はまだ続くが,とりあえず踏破した部分の色地図を描くと こんな感じになるだろう(図 4-6).
Prev: 3次元の場合
Next: 4次元の場合 (b)
Top: 画像付き版の最初
[ テキスト版 ]
[ 色覚テキスト Top ]