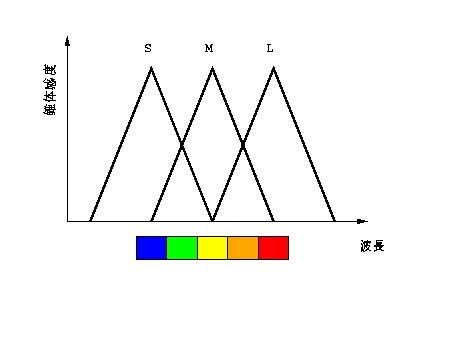
図 3-1 理想化した3種の錐体,S, M, L の波長感度特性
さて続いて3次元の場合.
人間と同じL, M, Sの3錐体を持つとしよう. この場合,錐体応答空間は (l, m, s ) の3次元になる. またそれぞれの錐体の波長特性はこんな感じ になっているとする.人間の場合と比べてだいぶ理想化してある.

図 3-1 理想化した3種の錐体,S, M, L の波長感度特性
例によって,さまざまな波長,さまざまな光強度の光刺激を与えたとき, 光応答を錐体応答空間 (l, m, s ) 上でどこにプロットされるか を表わしたのが図 3-2 だ.
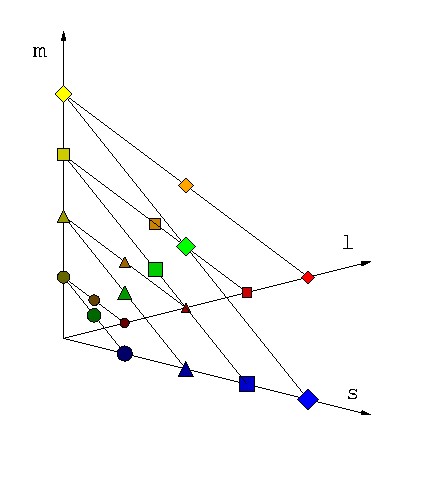
図 3-2 3次元の錐体応答空間.単波長光の光強度と波長を変えた時の軌跡を描いた.
光強度を一定にして波長を変えると,正三角形の2辺上を移動する. また光強度を変えると正三角形が原点から遠ざかり,大きな三角形を描くことが わかるだろう.
2次元の場合と同様に,錐体応答空間における光応答ベクトルと (1,1,1) ベクトルとの内積,すなわち l + m + s が「明るさ」に 相当する.そして光応答ベクトルが △LMS のどこを通過するかで「色」が決まる (図 3-3).
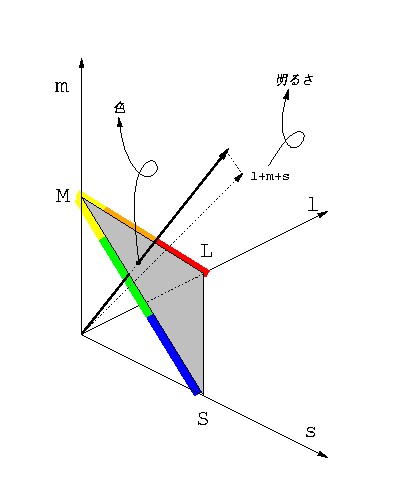
図 3-3 3次元の錐体応答空間では,原点からの距離が明るさに相当し,△LMSの通過点が色を表わす.△LMSを3原色の色空間と呼ぶ(ことにする).
すなわち3次元錐体応答空間の「色空間」は正三角形をした2次元空間になる (2次元錐体応答空間の「色空間」は線分LSの1次元空間だったことを 思い出してほしい).
また単波長光は必ず線分LM上か,あるいは線分MS上にしか来ない. 従って線分LS上や三角形の内部に相当する色は混合色(非単波長光)の持つ 色に相当する(図 3-4: 単波長光の合成によって △LMSの内部を通る光応答ベクトルを作れる様子).
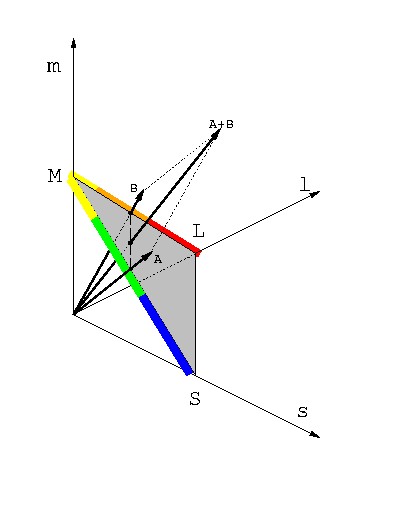
図 3-4 3次元錐体応答空間での混色.△LMSの内部を通るベクトルは混色のみによって作られる.
3次元錐体空間では,光応答ベクトルが△LMSを通過する点が「色」を表わすと 書いた.ここでいう「色」とは「明るさ」に依存しない「色合い」のことだ (たとえば赤は赤でも「明るい赤」「暗い赤」という違いはあるが,どちらも 明るさが違うだけで色合いは同じとする).つまり△LMSの上を隅から隅まで 探検すれば,3原色生物の感じることのできる色すべてに出会えるはずだ.
そこでさっそく,△LMSの上を探検してみようと思う. この探検は,3次元(錐体空間)生物であるヒトにとっては特に,大して エキサイティングなものにはならないが,しかし4原色生物の 色空間を探検する時の良い練習になるので,ここは手を抜かずやってみよう.
図 3-5 は△LMSの各点に 対応する色を書き込んだものだ.ここで書き込んだ色はヒトの感覚に合わせてある. (だから理想的な錐体応答特性の場合とは少し異なる).
まず単波長光に対する光刺激は線分LM, 線分MS上に存在する. そこでまず三角形の辺の上を探検してみよう. スタート地点は頂点S.ここは青紫の色がくる. ここから頂点Mへ向かって移動すると,
青紫→青→青緑→緑と連続的に色が変わって行く. 頂点Mに達したところで,今度は頂点Lへ移動してみよう.すると
緑→黄緑→黄色→橙→赤と連続的に変化しながら頂点Lに達する.
頂点Lから頂点Sまでの道のりに相当する単波長光は存在せず, ここは赤と青紫の単波長光の混色でしか表現できない. この辺をたどって行くと,
赤→赤紫→青紫と,この場合でも連続的に変化する.
ここで「赤紫」という色が出て来たが,この色について考えて見たい. そもそもこの名前からしてきわめて奇妙な色であることがわかるだろう. なにせ最も波長の長い赤と,最も波長の短い紫が混じってひとつの色として 感じられるのだから. もし2原色生物が「赤紫」という色を聞いたらさぞかし驚くのではなかろうか. なぜなら2原色生物にとって色空間は線分LSの1次元であり,その両端である 青紫と赤は対極の色になるからだ.その2つが「赤紫」という色を介して連続的に つながるとはとても思えないだろう.
しかし3原色生物にとって「赤紫」という色が自然に存在してしまうということが, 4原色生物の色感覚を考える時のポイントになる. つまり,われわれ3原色生物にとって不可思議な色であっても,彼らには 自然な色として存在することが予想されるからだ.
さて△LMSに話をもどそう.この三角形を風船に見立てて,ふーっと息を吹き込んで 膨らませてみよう.すると丸い形になるはずだ,こんな感じに.
これがいわゆる「色環」だ. 実際のわれわれの日常感覚としては, 「頂点」という特別な点がある 三角形モデルよりも, 原色がすべて対等の関係を保って環形に並んだ色環モデルの方が 自然に思えるのではなかろうか.
なお,実際の人間が感じる色空間については心理学的に詳しく調べられており, 有名なCIE色度図が その代表的な存在だ.CIE図の馬蹄形をした領域が,今までの話の △LMSとまったく同じものである.
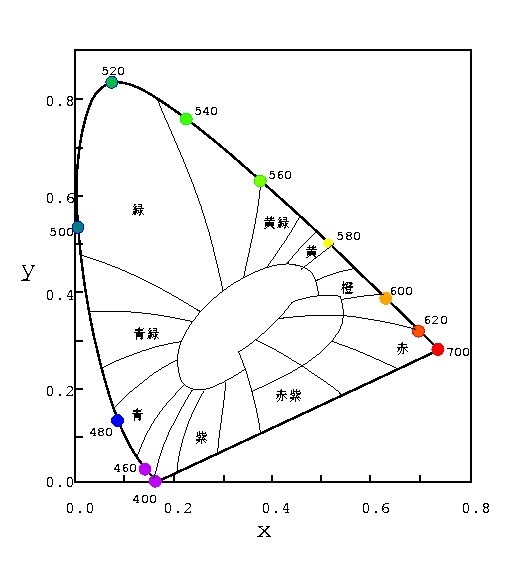
図 3-7 CIE色度図.
△LMSの探検をもう少し続けよう.
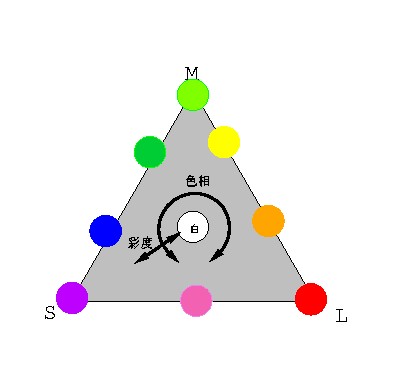
図 3-5 3原色色空間の探検.(再掲)
先程は三角形の辺に沿って探検したが,今度は内陸部に分け入ってみる.
まず一足飛びに三角形の中央.ここはすべての光を足し合わせた時に生じる色だから 「白」に相当する.もっともこの三角形では「明るさ」を考慮しないので, 灰色と言った方がより正確だろう.
ではこんどは三角形の辺上,つまり沿岸部から内陸部へ連続的に移動してみよう. このとき重要なことは,「色空間を連続的に移動した時に感じる色は,やはり 連続的に変化して感じる」ということだ.たとえば頂点Sから三角形の中央へ 連続的に移動すると,最初は「鮮やかな青紫」だったのが,徐々にくすんで 「灰色がかった青紫」に変わり,次いで「少し青味を帯びた灰色」になり, 最後は完全に「灰色」になってしまう(この間,「明るさ」の変化はないことに 注意.色合いのみが変化する).これは他の点からスタートしても同じだ.
このことから次のことが言える.三角形の中央を原点としたとき,中央から どちらの方向に光応答のベクトルが通っているかで色合いが決まる.また ベクトルの位置が三角形の中央からどれくらい離れているかで「鮮やかさ」 が決まる.離れれば離れるほど鮮やかな「原色」に近くなる. このように「鮮やかさ」のことを「彩度」と言い,「色合い」のことを「色相」 と言う.つまり私たちは2次元の色空間を「色相」と「彩度」という二つの要素に 分解して,一種の極座標表示のように感じていることがわかるだろう. (極座標的な感覚は色環モデルの方がより明確だ).
一般に,混合色は三角形の内部に入り込むので彩度が落ちる. ただし赤紫は例外的な色で,これは三角形の辺上に位置し, 単波長光と同じ鮮やかさを保っている.すなわち原色のひとつとして「赤紫」が 仲間入りしたと考えられる(このことも4原色生物について考える時の ヒントになる).
△LMSの探検をさらに進めてみよう. 「色空間内部で連続的に移動すると,知覚される色も連続的に変化する」 ということを念頭に置いて探検してみる. たとえば青紫から緑への変化は,青・青緑を経由して連続的に緑へとつながる. では「青から黄色」はどうか.この場合,△LMSの中央を通過する. したがって
青 → 灰色がかった青 → 青みを帯びた灰色 → 灰色 → 黄みを帯びた灰色 → 灰色がかった黄色 → 黄色というプロセスを経る.このようにいったん色味を帯びない無彩色を経由して 初めて青から黄色へと変化しうる.
このようなプロセスは赤→緑の場合も生じる.円環上で向かい合わせの色を 「反対色」と呼ぶが,反対色ペアの特徴は,「その2つの中間の色を想像することが できない」ということにある(なぜなら,両者の中間の色は灰色になるのだから). たとえば「黄青」とか「赤緑」という色を想像することはできないだろう. それに対して「黄赤」と言われたら「橙色」を思い浮かべるのではなかろうか.
3次元の場合の反対色について考えてみよう.
2次元の場合もそうであったが,錐体空間 (l, m, s ) から 明るさの情報と色の情報を分離する時に反対色が生じると書いた. 3次元錐体空間から 明るさの情報を取り出すように座標変換してみよう. 3次元の場合,いろんな変換が考えられるが, たとえばこんな具合だ.
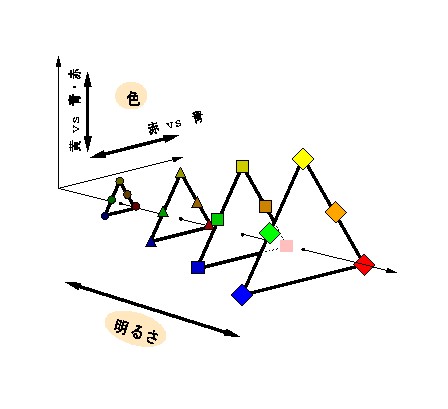
図 3-8 3次元錐体応答空間を座標変換し,明るさと色の情報を分離する.
図 3-8 を見てわかるとおり,明るさを除いた色空間の次元は2次元だ. したがって色空間上の位置を指定するには2本の座標軸が必要になる. 図 3-8 の場合,それぞれが赤 vs 緑の反対色,赤・青 vs 黄の反対色に なっている.すなわち色空間上の座標を指定するには,色空間の次元数と 同じ数の反対色ペアが必要になる.
図 3-a はコイの網膜2次ニューロン (水平細胞)の光応答波形だ (A. Kaneko, Jpn. J. Physiol. 37, pp.341-358, 1987.).
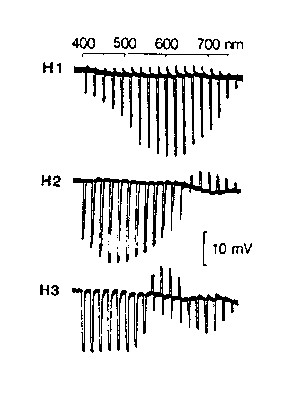
図 3-a コイ網膜の2次ニューロン(水平細胞)の光応答記録例.波長を変えながら光刺激をフラッシュ状に与えた.H2, H3は反対色応答を示す(A. Kaneko, Jpn. J. Physiol. 37, pp.341-358, 1987).
コイは錐体入力型の水平細胞を3種持ち,H1が明るさ型, H2が赤vs緑反対色型,H3が赤・青vs黄反対色型になっている. またこのような光応答特性のメカニズムはこのようなモデルで 表わせる(明るさチャネルが l + m + s ではなく l のみに なっているのは理由があるのだが,その説明は省く. この点はあまり気にしなくて良い).
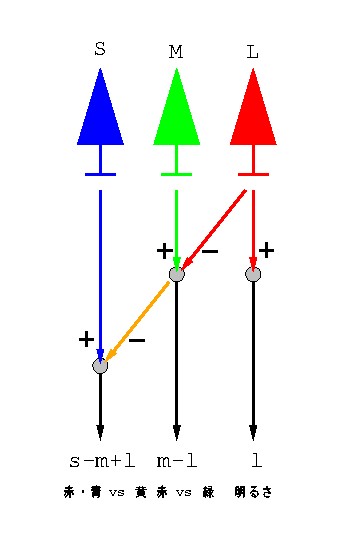
図 3-9 コイの水平細胞で反対色応答が作られるメカニズムを示したモデル.
ヒトの場合も似たように,1つの明るさチャネルと2つの反対色チャネルを持つ. ヒトの場合は進化的な事情があってややこしいので,ここでは出さないが, 言いたいことはこうだ. 色空間がn次元ならば,n個の反対色チャネルが必要になる, ということだ.たとえば錐体を3種持っている生物がいたとして,反対色チャネルを 1つしか持っていなかったとすれば,その生物が本当に3次元の光応答空間で物を 見ているかは疑わしい.
このことを,やはりコイを例にして説明しよう. コイは赤・緑・青錐体の他にUV錐体を持つ (……と思ったが,公式にUV錐体の存在が報告されているのは コイではなくキンギョだった.が,キンギョとコイの網膜は区別がつかないほどよく 似ているので,この場ではその違いを気にする必要はない). ということは4次元の錐体応答空間を 持ち,3次元の色空間を持つことが期待できる.ところがいくら探しても反対色 チャネルは2つしか見つからない.どうやらUV錐体の応答は青錐体の応答と加算され て2次ニューロンへ伝えられているように思える.もしそうだとすると,UV錐体は 単に青錐体の帯域幅を広げるためにしか役立っていないことになる. このような場合,いくら4種の錐体があっても,事実上は3種(そのうちのひとつは 帯域幅の広い青錐体)しかないのと変わりがない.
3次元の場合の混色も2次元の場合と同様だ.
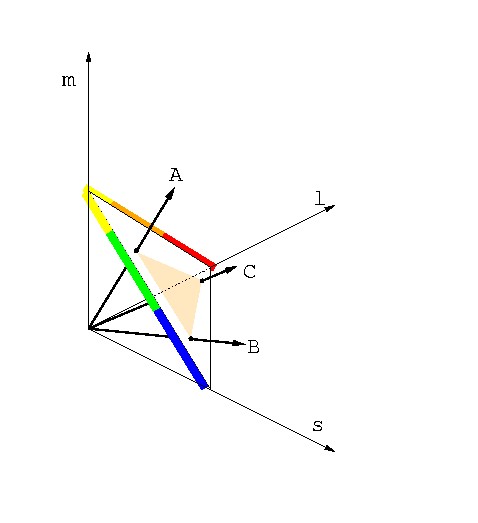
図 3-10 A, B, C の3つの光の合成で表現できる色は,3つのベクトルで囲まれた領域内に限られる.
(l, m, s ) 空間上の 3つのベクトル A, B, C を任意の強度で足し合わせることで表現可能な光は, 3つのベクトルにはさまれた領域になる.明るさは強度を変えればいくらでも 変えられるが,色はA, B, Cの3つのベクトルが色空間を横切る3点で囲まれた 三角形の範囲しか表わされない.
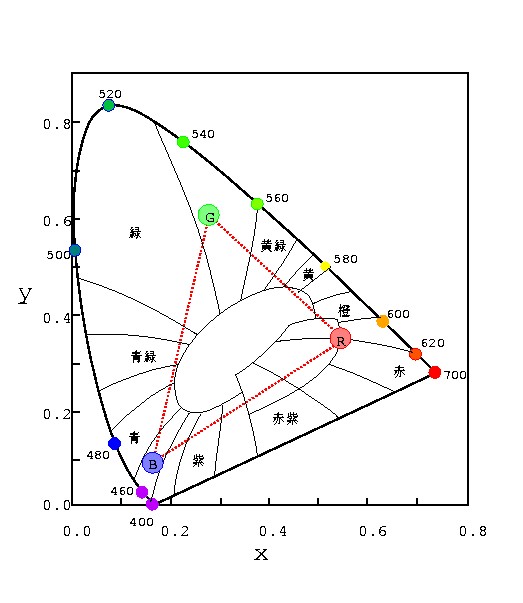
図 3-11 CIE色度図上で示した,ブラウン管ディスプレイの3原色の座標.この三角形内の色のみを表現できる.
これはCIE図の上に典型的な ブラウン管モニタの3原色R, G, Bの位置を書き込んだものだ. すなわちブラウン管上で表現できる色は図中の三角形の内部になる.
よく「3原色あればすべての色を表現できる」と言われるが,正しい言い方ではない. 光応答空間が3次元だから,最低3つのベクトルが必要だと言うことにすぎない. (理想的な錐体応答特性を持つ場合は色空間が正三角形になるため, その頂点をベクトルとする色を3つ選べば「すべての色を表現できる」 ことになる). ブラウン管の場合,もうひとつ電子ビームを増やして4つの光の混色で表わせば, 今度は四角形で囲まれた領域を表現できることになる.その方がずっと表現できる 幅が広がる(最近,カラーフィルムで4つの層で表現するものが出て来たが 同じ話だ).
これでほぼ3次元の光応答空間の探検をし終えたように思う. 次回からいよいよ4次元へと進んでみたい.
Prev: 2次元の場合
Next: 4次元の場合 (a)
Top: 画像付き版の最初
[ テキスト版 ]
[ 色覚テキスト Top ]