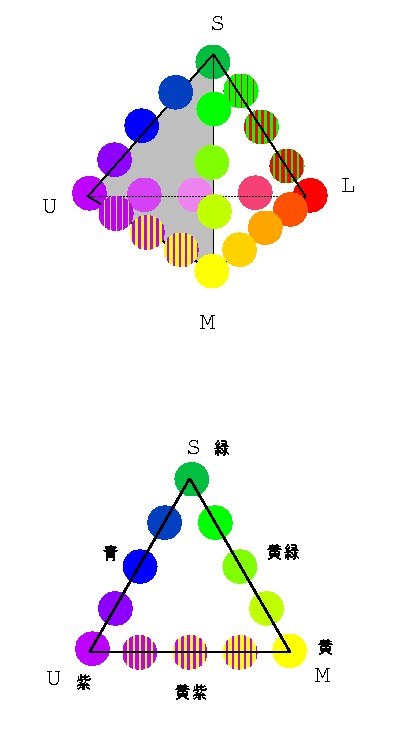
図 4-7a △USMの探検
さて,正四面体の辺上は すべて探検しおわった. 次は正四面体の各面を考えてみよう.
まず面USMを考えてみる(図 4-7a).
この面は紫・緑・黄を3頂点とする正三角形だ.そして紫−緑ラインの中間は青, 緑−黄ラインの中間は黄緑,そして紫−黄ラインの中間は先程出て来た黄紫だ.
さて,先程と同じように,今度は各頂点から出発して向かいの辺まで連続的に 移動してみよう.まず黄→青と移動してみる.すると黄色から青まで,三角形 USMの中心を通って連続的に色が変化する.そこで便宜上,この面の中心の色を 黄青と呼ぶことにしよう(この色も原色のように鮮やかに感じられるはずだ). 以降,図 4-7aを見ながら以下の 説明を追ってもらいたい.
例によって黄から青への変遷を連続的に追ってみる.
黄色となることだろう.黄青という色もまったく想像しにくい色ではあるが, それについてはあまり悩まずに次に行ってみよう.
↓
黄がかった黄青
↓
黄青
↓
青がかった黄青
↓
青
では今度は別のルート,「紫から黄緑」を考えてみよう. (図 4-7aで言えば 左下から右上へのルートだ).この場合,色は次のように変遷することだろう.
紫という具合になる.青みの成分が紫から徐々に緑へと変わり,同時に黄色味を 帯びてくるという感じだ.ここで「黄緑がかる」と単純に言い切らず,あえて 「黄色と緑がかる」という言い方をしたのはわけがある.それは最後のケース, 「緑から黄紫」へのルートを考える時に便利だからだ.
↓
少し黄色と緑が同時にかかった紫(黄緑がかった緑)
↓
紫がかった黄青
↓
黄青
↓
黄色と緑がかった黄青(黄緑がかった黄青)
↓
少し紫がかった黄緑
↓
黄緑
では最後に「緑から黄紫」を考えてみる. (くどいようだが図 4-7aを 常に参照してほしい).三角形の垂直のルートだ.この場合,上へ行くほど緑が, 下へ行くほど黄色と紫の色が強くなる.この場合,「黄紫がかる」という言葉が 想像不可能なので,上の「紫から黄緑」のケースに倣い,単に「紫」を「緑」に, 「黄緑」を「黄紫」と言葉を置き換えてみよう.することこんな感じになる.
緑このように,色としては想像しにくいものの,やはり筋の通った変化を 示すことがわかる.
↓
少し黄色と紫が同時にかかった緑(黄紫がかった緑)
↓
緑がかった黄青
↓
黄青
↓
黄色と紫がかった黄青(黄紫がかった黄青)
↓
少し緑がかった黄紫
↓
黄紫
黄青を中心にした面上の色の変化はまったく想像しにくいものの, それでも全体として矛盾なく成立していることには気づいてほしい. たとえば上で挙げなかったようなルート, たとえば「黄紫」から「黄緑」へ移動する場合でも
黄紫というルートを通るはずで,これも筋が通った変化だ. なぜなら「紫と緑の中間が青」ならば, 「黄紫と黄緑の中間は黄青」となることが予想されるからで, 「黄」の成分を一定に保ったまま「紫の成分が緑の成分へ」変化するような形で 色合いも変化すると考えられるからだ.
↓
(やや黄がかった)黄青
↓
黄緑
同じことの繰り返しになるが,これらの色が「どんな色に見えるか」を直接想像しても できるわけはない.むしろ4原色の色は互いにこんな特徴を持って感じられるのだな, と考えながら想像してほしい.
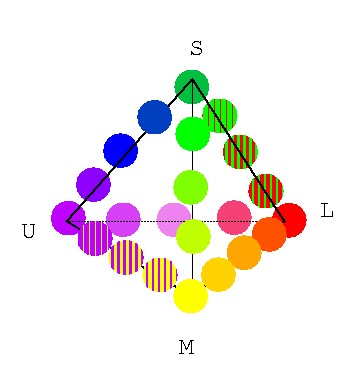
図 4-6 4原色色空間の各辺の色を表わした図.(再掲)
まず三角形SML.
この場合,面の中央は橙緑と呼ぶのが適当であろう. この面内で色ベクトルをさまざまに連続的に動かし, たしかに「赤青」という色をはさんで矛盾なく色が変わってくれることを確かめて ほしい(4次元の色を感覚的に理解したいのならば,結局は自分でいろいろ やってみる他にしようがない.誰かがその感覚だけをぱっと伝授できれば 本当に楽なのだが).
続いて三角形SLU.
この場合,面の中央の色は赤青と呼ぶことにしよう. 同じように各自いろいろ試してもらいたい.
最後は正四面体の底面,三角形MUL.
この面の中央は橙紫と呼ぶのが適切だろう.
これで各面の中央の色が出揃ったわけだが,同時に各面のすべての色についても 探検しおえたことになる.
4つの面の中央の色は,黄青・橙緑・赤青・橙紫の4色だった. 実はこれらの4色が減法混色の4原色になる.
3次元の色空間(図 3-5)を丸く膨らませると色環(図 3-6)ができた.
わたしたちの感覚では,3つの色を頂点とした三角形よりも, むしろ原色が環状に並んだ方が近いかもしれない. 4次元の場合も同じように考えることができるだろう. この場合, 球面の上にさまざまな色が並ぶことになる.
球面上の色の配置を図で示すのは,世界地図と同じ問題でやさしくない. ためしに緑を北極にした地図 を描いて見た(cf. 正四面体で描いた場合).
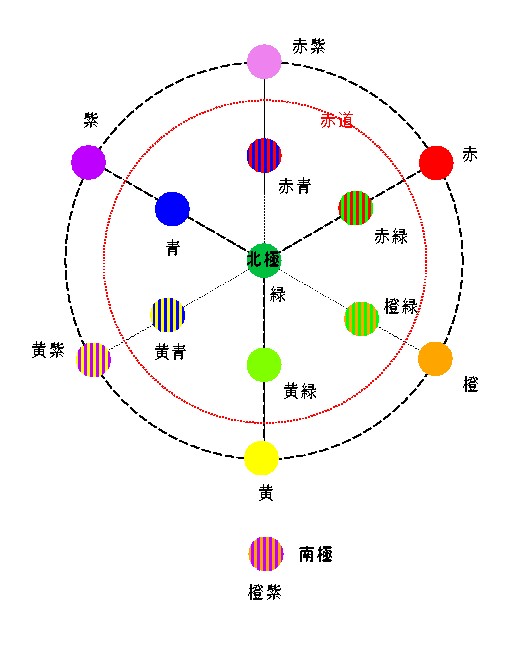
図 4-12 緑を中心(北極)にしたときの色球の正距方位図法表現
図 4-12では同心円状に色が並んでいるが,外側の円周と内側の円周の 間に赤道が来る(だから外側の円周上の色は本当は見えないはずだ). 南極は橙紫.つまり緑と橙紫は反対色の関係にあると言える(緑と橙紫を 混ぜると灰色になる).なお正三角形の辺に相当する部分を太い破線で示した.
逆に橙紫を南極にして同じ図を描いたのが図 4-13 だ.
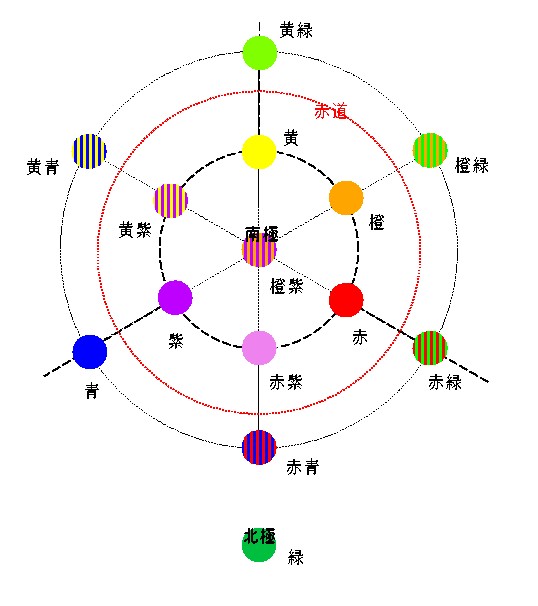
図 4-13 橙紫を中心(南極)にしたときの色球の正距方位図法表現
これら2つの図(図 4-12, 図 4-13)はあくまでも緑と橙紫を中心に描いたもので, 中心からの方角と距離は(おおむね)正しい. したがって中央の色とその他の色との相互関係を知るには便利だが, 残念ながら中央以外の色同士の関係は正しく示していない. たとえば外周に行くほど隣の色との間隔が広がるが, 実際にはそのようなことはない.
このような地図は色空間の任意の点を中心にして同じように描くことができる.
さて,先程の地図(図 4-12) では,中心になる色と他の色との位置関係はわかったが,任意の色と色との 位置関係はわかりにくかった.そこでもう少し良い色球の表記方法はないか 考えてみよう.
3原色の場合,三角形の頂点に加法混色の3原色が来る. そして各辺の中央に減法混色の3原色が来る. この二つの三角形をちょうどダビデの星のように重ねて正六角形を作ると, 色環上の色をちょうど60度ずつサンプリングしたような形になる.
これと同じことを色球でもやってみよう.
2つの正四面体の8つの頂点がちょうど等間隔に並ぶように配置すると, 正六面体ができあがる(逆に,正六面体の頂点をひとつとばしにつなげると 2つの正四面体になる).4原色の色空間である正四面体の各頂点に相当するのは 加法混色の4原色である紫・緑・黄・赤が並ぶ.それに対して4つの面に相当するのは 減法混色の4原色である黄青・橙緑・赤青・橙紫である.これら8つの点が 立方体の頂点に来るように配置する.また正四面体の6つの辺上の色は, ちょうど正六面体の6つの面の中央に位置する.
この方法で図にするとこうなる(図 4-14, 4-15, 4-16, 4-17).この図では90度ずつ回転させてみた.
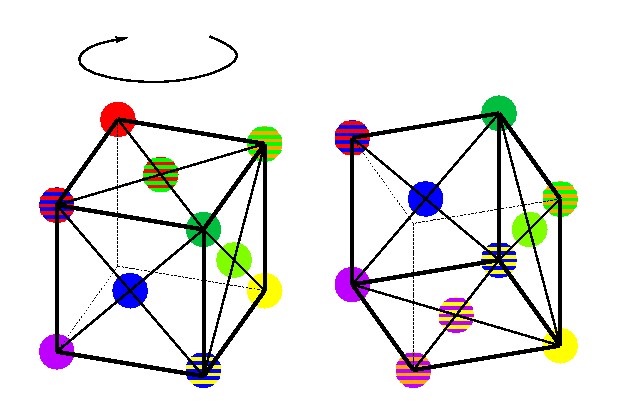
斜め上から見たところと,斜め下から見上げたところ.
以下,90度ずつ回転していく.
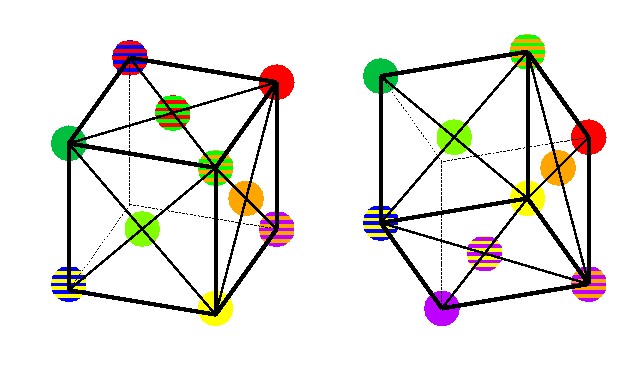
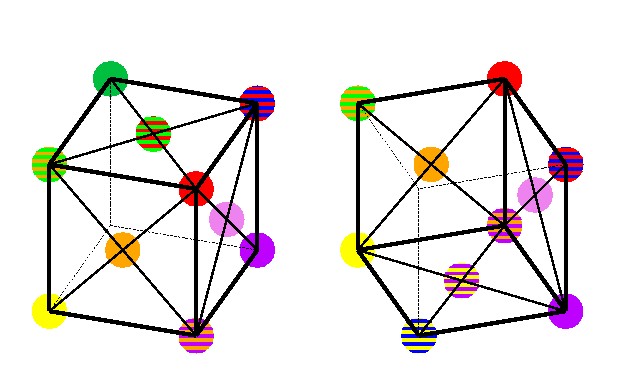
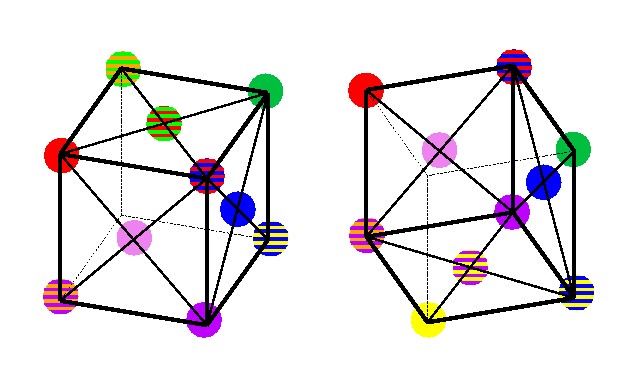
図 4-14, 4-15, 4-16, 4-17 立方体で表現した色球.左右のペアはそれぞれ斜め上/下から見たもの.各段は90度ずつ回転させた時の図を示している.
このように表示することで 4原色空間の色の相互的な位置関係が正四面体の場合よりずっとわかりやすくなる. 正四面体の場合,辺を乗り越えて隣の面との色の相互関係を見るのが難しかったが, この図ではそれがずっと見やすくなっている.できるならもう一度,この図の上で 色の探検をしてほしい.
ところでこの4原色空間の色立方体の上で,単波長光がどのように配置されているか 追いかけてみると,かなり複雑な軌跡を描くことがわかる.どうも4原色空間では 単波長光を単純な座標変換で取り出すことはできないのではないかと思われる.
Prev: 4次元の場合 (a)
Next: 4次元の場合 (c)
Top: 画像付き版の最初
[ テキスト版 ]
[ 色覚テキスト Top ]