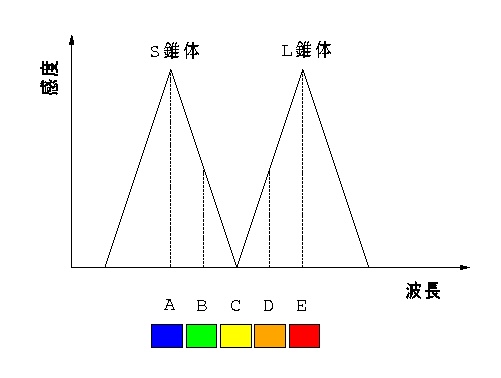
図 2-1 理想化した2種の錐体,S, L の波長感度特性(1).互いの特性にオーバーラップがない場合.
つぎに2種の錐体(LとSにしよう)を持つ場合について考える. この場合,L・S錐体の波長感度特性に オーバーラップがない場合と オーバーラップがある場合 の2とおりに分けて考えてみる. まず最初はオーバーラップがない場合.

図 2-1 理想化した2種の錐体,S, L の波長感度特性(1).互いの特性にオーバーラップがない場合.
2種の錐体L, Sを持つ場合,光応答は (l, s ) という2次元の錐体応答空間上で表わされる. では1次元の場合と同様に,光の強度や波長をさまざまに変えた時 (強度: 1〜4,波長: A〜E),それぞれの光応答が (l, s ) 空間上の どこにプロットされるかを見てみよう.
図 2-2 がその結果だ.
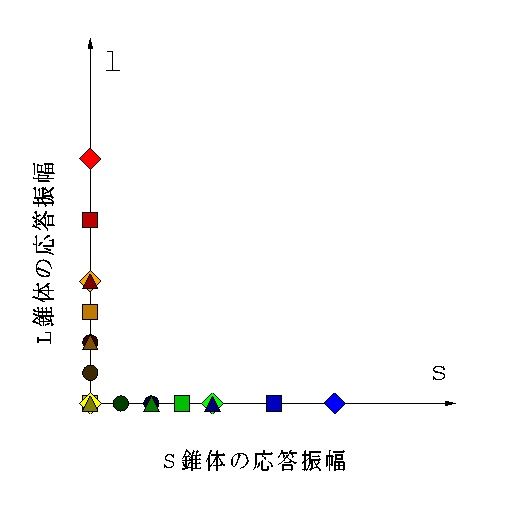
図 2-2 図2-1の錐体特性によって生じる2次元錐体応答空間.単波長光の光強度と波長をさまざまに変えた時の各光応答ベクトルの座標を示した.
図 2-2 を見てもわかるとおり(そして当然予想されるべき結果として), すべての点は2本の座標軸のどちらかの上にしか来ない. そしてそれぞれの座標軸上では,波長の違いと強度の違いが区別できない.
つまりL, S錐体を分ける波長Cを境にして,単波長光の光刺激がどちらの領域に あるかは区別できるものの,それぞれの領域においては1錐体の場合と同じ話に なってしまうというわけだ.したがってヒトならば 図 2-3 の上段のように見えるところが, この生物には下段のように見えることだろう.
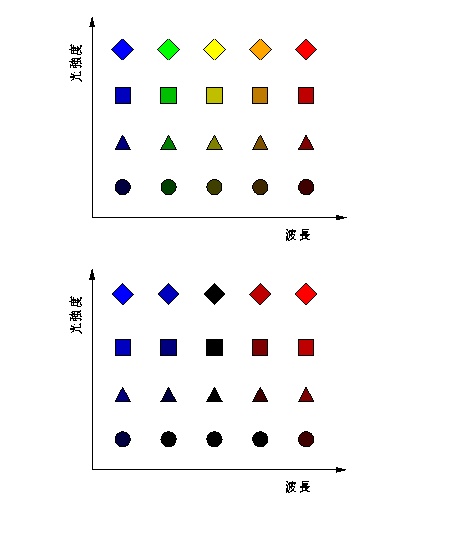
図 2-3 図2-1の錐体特性によって生じる色知覚.上段がヒトのもの,下段が図2-1の錐体を持つ動物.
2次元の場合(1)について少し補足. 補足と言ってもよりわかりやすくするための補足ではなく, より話を複雑にさせるための補足だが.
錐体の波長特性にオーバーラップがないと,確かに単波長光の 波長と強度を区別することはできない.しかしだ. 世の中,単波長光ばかりとは限らない.いやむしろ単波長光の方が珍しく, 連続スペクトルを取る場合の方がふつうた. もし光刺激の波長分布についてあるなめらかさが保証されるなら, つまり波長が変わってもスペクトルは急激に変わらず,その結果として, L錐体もS錐体も刺激するのであれば,波長特性にオーバーラップがなくても なんら困らない.
非常に極端な例だが,錐体の感度が特定の波長のみにしか存在しない場合を考え てみよう.たとえば600nmの光にしか感じない錐体だとか,500nmの光にしか感じ ない錐体を想定する.それに対して光刺激のスペクトル分布 S(λ) は,100nmの オーダーでゆっくりとしか変わらないとする.このような状況は,要するにスペ クトル分布 S(λ) を500nmや600nmの点でサンプリングすることに相当する. それはそれでまったく困ったことにはならないことがわかるだろう.
実際,ランドサットなどの衛星が地上を観測する時は,地球が放射する電磁波を いくつかの波長においてサンプリングしているにすぎない.観測対象次第では それでもかまわないのだ.
また2次元の場合(2)で述べる「波長感度にオーバーラップがある場合」は,単波長光と合成光を 区別することができない.それに対して2次元の場合(1)の「オーバーラップがない場合」は両者を 区別することができる.以上のような理由により,「オーバーラップがないと色を 見分けられないから不利」という説明は(よく見かけるし,私自身もそう説明して すませることもままあるけれど)もっともらしいが必ずしも正しくない.
続いて2種の錐体の波長感度特性に オーバーラップがある場合.
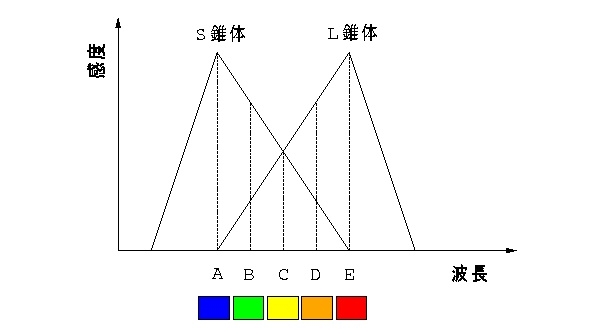
図 2-4 理想化した2種の錐体,S, L の波長感度特性(2).互いの特性にオーバーラップがある場合.
この場合も錐体応答空間は (l, s ) の2次元だ. 今までと同じように,さまざまな光強度(1〜4),さまざまな波長(A〜E)の 光刺激が (l, s ) 上のどこにプロットされるかを見てみよう.
図 2-5 がその結果.
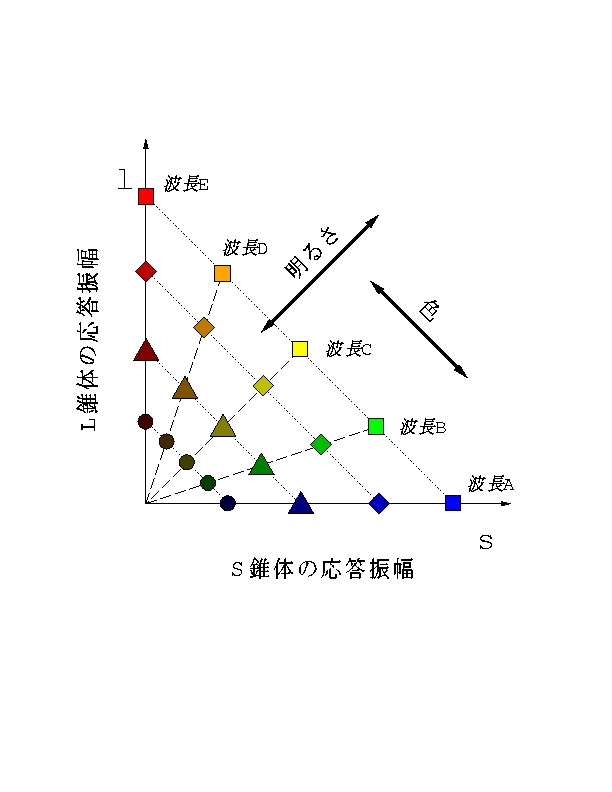
図 2-5 図2-4の錐体特性によって生じる2次元錐体応答空間.
ご覧になってわかるとおり,ここに来て初めて,単波長光の波長の違いと 強度の違いを分離してプロットすることができた.
図 2-5 を見ればわかるとおり, 光強度が強くなれば原点から遠くなる.また原点からの方角が波長の情報を もたらす(それぞれ「明るさ」「色」と言った方が良いだろう).これを もう少し正確に書くと図 2-6 のようになる.
今,ある光刺激によって生じた光応答のベクトルを C とする.このとき,C と (+1, +1) ベクトルとの内積が「明るさ」に 相当する.また C が線分LSを通過する点が「色」を表わすと言える.
ここで,線分LS は色あいのみを表わした空間(すなわち明るさは一定とした時の 色を表わす空間)と考えることができる.この線分LSを今後 色空間 と呼ぶことにする.一般に n 次元の錐体応答空間の色空間は (n-1) 次元になる (明るさは常に1次元なので).すなわちヒト(3次元)の場合の色空間は 2次元になるだろうし,4錐体生物の色空間は3次元になると予想される.
オーバーラップのある場合について引き続き考えてみよう.
錐体の波長感度にオーバーラップがあれば,単波長光の波長の違いと強度の違いを 「色」と「明るさ」という形で区別できることがわかった.もっとも区別できるのは わたしたちが (l, s ) 上にプロットされた点を眺めているからであって, 当の生物本人にとっては依然としてL錐体とS錐体の情報がそれぞれ別個に入って きているだけだ.そしてL錐体の応答 l のみを見ても,また S錐体の応答 s のみを見ても「色」や「明るさ」を知ることはできない.
そこで次のような線形変換を考えてみる.
x = l + sすると (l, s ) 空間は図 2-7 のように -45度 回転する.
y = l - s
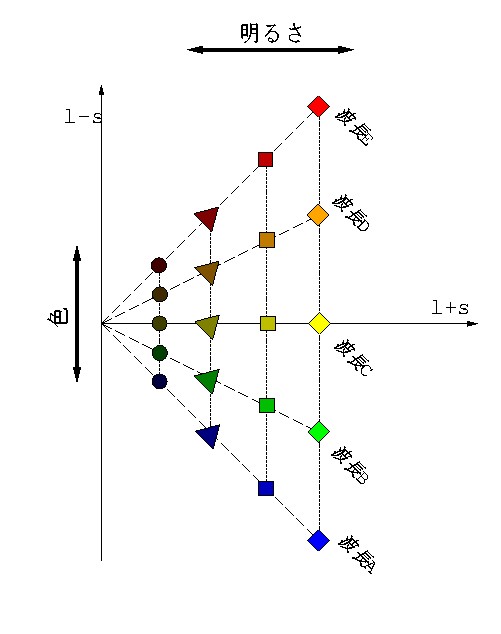
図 2-7 2次元錐体応答空間を座標変換して,明るさと色を分離する.
こうすれば x軸 は光刺激の波長に依存しない明るさ情報を伝えることがわかるだろう. また注目してほしいのは y軸 だ.y の符号は短波長(青)側でマイナス, 長波長(赤)側でプラスになり,符号が反対になる. すなわちy軸は反対色を意味する.
これを神経回路で表わすとこんな感じになるだろう.
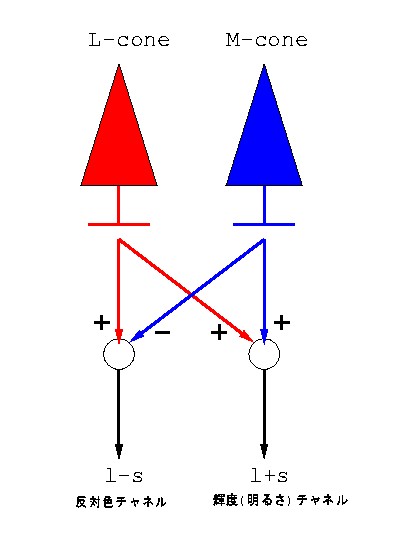
図 2-8 図2-7の座標変換に相当する神経回路モデル
錐体から入力を受けるニューロンには2種類あり, L, S錐体の双方から興奮性入力を受けるl+s ニューロンの方は 明るさチャネルを作り,S錐体から抑制性の入力を受けるl-s ニューロンの方は 反対色チャネルを作る. このような2つのチャネルの存在は実際にもよく知られている.
厳密に言うならば,l-s のみでは「色」を表わしたとは言えない. なぜなら l-s の値は単波長光の波長のみならず強度にも依存するからだ. 強度に対する依存性をなくすのであれば,(l-s )/(l+s ) という 変換をすれば良い.こうすると (l, s) 空間上のプロットは 図 2-9 のように変換され,完全に明るさ情報と色情報に分離される.
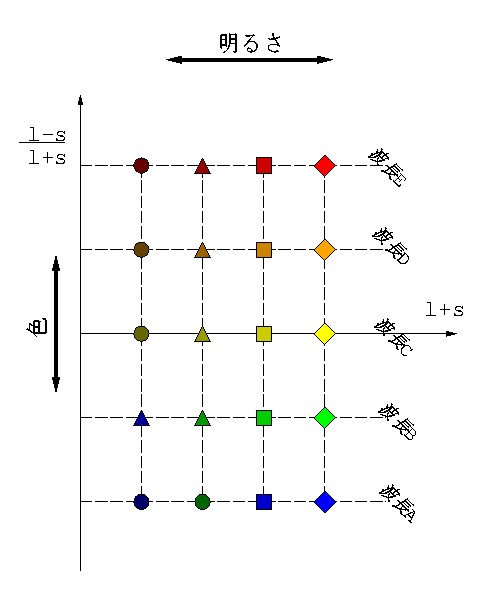
図 2-9 図2-7の縦軸を明るさで規格化すると,縦軸は色合いそのものを表わす.
これを神経回路で書けばこんな感じになるだろう.
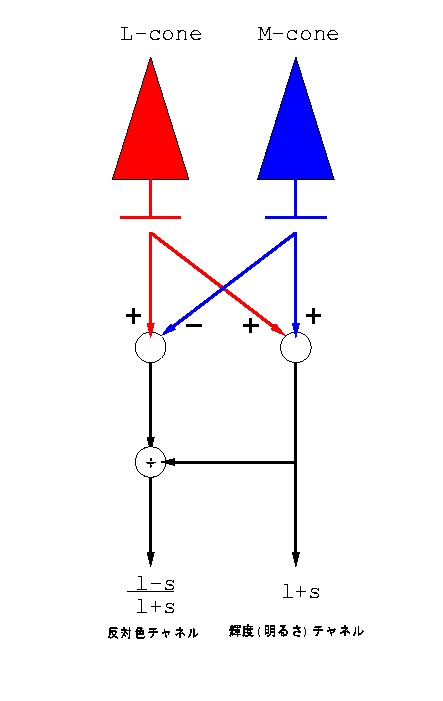
図 2-10 図2-9に相当する神経回路モデル.
もっともこのように l+s でノーマライズされた応答は網膜の段階では 見られないのだが.
2錐体系では,色空間の次元が1次元になると述べた (図 2-6 の線分LS). (l-s )/(l+s ) で示す値は,光応答が色空間(線分LS上)の どの点に位置するかを表わしている(図 2-11).
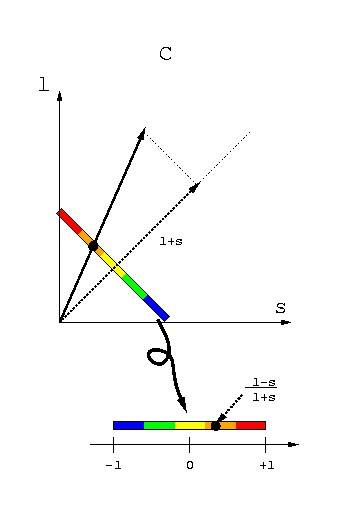
図 2-11 座標変換によって色空間上の座標を抽出する.
今までは単波長光についてのみ考えてきたが,ここで混色について考えてみよう.
今,光刺激AとBがあるとする.それぞれ (l, s ) 空間上での ベクトルは図 2-12 のようになる.
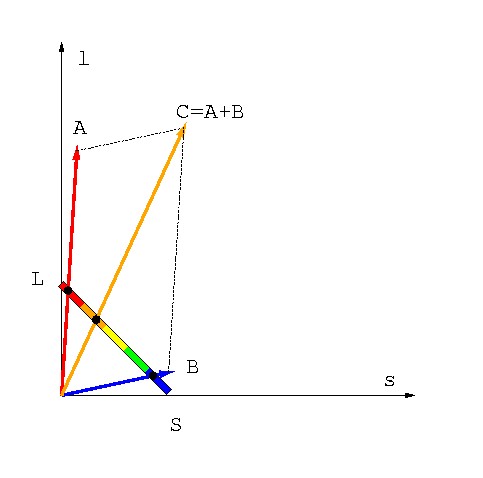
図 2-12 2次元錐体応答空間における混色
両者が同時にやってきた時に生じる光応答は(錐体応答特性の線形性を 仮定すれば)Cのようなベクトルになる.したがってA(赤)とB(青)の 光を(赤の方を多めに)混ぜると,橙色に見えるはずだ.
ベクトルCと同じ光応答は単波長光を用いて起すこともできる. すなわちA+Bによって生じた光応答と,橙色の単波長光Cとを区別することは できない(まったく同じ光として感じる).
2次元空間上の任意のベクトルは,一次独立な2つのベクトルの線形和で 表わされる.すなわち波長の異なる2種の単波長光があれば,それ以外の 波長の光によって生じる光応答を再現することができる.つまり2原色あれば 明るさと色の表現が可能になる.
ただし光の線形加算では,係数は正もしくはゼロしか認められない.
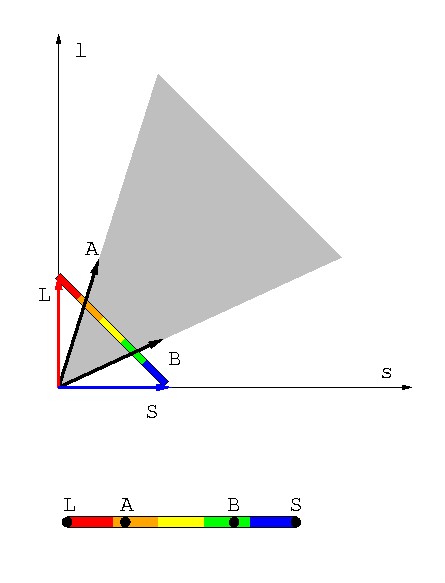
図 2-13 2つの光の混色で表現できる光応答ベクトルの範囲
たとえば図 2-13 の ベクトルA・Bに相当する光刺激を基ベクトル(2原色)とした場合, 2つのベクトルではさまれた領域(グレーの部分)のベクトルしか 再現できない.この場合,ベクトルL・Sを選べばすべての光応答を 再現することができる. 同じ話を色空間(線分LS)上で考えてみよう.色空間の上で言えば, ベクトルA・Bの混色によって作れる色は,色空間上の点Aと点Bの 間にある色だけだ.この区間外にある色は作れない.色空間の両端に あるLとSを使えば,混色ですべての色が表現できることになる (図 2-13 の下段).
Prev: 前書き・1次元の場合
Next: 3次元の場合
Top: 画像付き版の最初
[ テキスト版 ]
[ 色覚テキスト Top ]