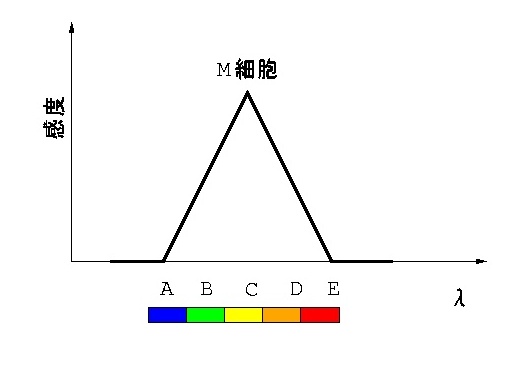
図 1-1 理想化した錐体Mの波長感度特性
※L, M, Sはそれぞれ long-, middle-, short- の頭文字で,L錐体が3つの中 でもっとも長い波長の光(赤側)に最大感度を持ち,S錐体がもっとも短い波長 の光(青側)に最大感度を持つ.M錐体はその中間だ.
今,色について考えたいので,光の空間分布(つまり物の形)は考えないとする. 視野全体に同じ光を一面与えた場合について考える.そしてL, M, S錐体の光応 答振幅をそれぞれ l, m, s とすると,すべての光刺激に対する視細胞 の応答は (l, m, s ) の3次元ベクトルで表わされる.これをここでは 3次元もしくは3原色の錐体(光)応答空間(あるいは単 に空間)と呼ぶことにする.
もし錐体応答空間が2次元(すなわち2原色)ならば,その生物にとってすべて の光刺激は2次元空間上に記述できる.そしてこの場合も色を感じることはでき るが,それは私たちの感じ方と異なる.同様に4種の錐体を持つ生物がいたとす るならば(実際そのような生物も存在するのだが),その生物は4次元空間で光 を感じることができる.4原色の色彩は,われわれ3原色の世界に棲む生物にとっ て感じることのできない色の世界だ.しかし,4次元の色そのものは感じること ができなくても,色覚の情報処理過程を考えることで,4原色生物が4次元の色 をどう感じているかについてくらいなら想像する手がかりがある.そこでそれら 手がかりを元にして4原色生物の色覚を考えてみようというのが,本テキストの 目的である.
そこで本テキストでは,まず錐体が1種しかない生物,すなわち1次元錐体応答 について考え,光応答がどのような特性を持つか調べてみる.同様に2次元,3 次元の場合についても調べてみる.このとき,どの次元もなるべく同じ方法 で調べてみよう.なぜなら次の段階では4次元の光応答空間を同じ方法で調 べるわけであり,1〜3次元の場合はその予備練習に相当するからだ.すなわち 1〜3次元の場合は,すでに確立している色覚についての話を,非常に簡潔にま とめたものとなっている(したがって色覚について詳しい人はこれらを斜め読み してもらってかまわない).そして最後に4次元の場合について同じアプローチ で解析することで,4原色生物の色覚情報処理について考察し,そこから彼らが どのように色を感じているかを推測してみようと思う.
このテキストはWeb上の掲示板: 「ふるかわ通信板」に私が投稿したものだ.し かもこの投稿は全体の構成や推敲をした後に投稿したものではなく,思いついた アイデアを記録する,いわばメモ代わりとして投稿したものだ.原文は一気にタ イプしたままであり,読み返すことすらほとんどしていない.特に4次元の場合 はそれが顕著で,ほとんど思いつくままに書いたので説明の順番が適切でない箇 所が方々に見られる.また用語の統一も図られていない.文体もつっけんどんで 愛想のない文と思われるだろうが(特にこの前書き),このような事情によるも のと思って勘弁してほしい.いずれは本文・図ともにきちんと書き換えられるべ きと思う.
本テキストではまた,話を明確かつ単純化するため,方々で細胞の特性の理想化 を行っている.これらの操作によって本質が失われることはない.しかし,この 操作によって個々の生物種の視覚系に依存したもろもろの現象は失われた(とい うか,むしろ積極的に切り捨てた).それらは色覚の理論を学ぶ上では非本質的 であり,話をややこしくする張本人であるからだ.特にヒトの色覚は話をややこ しくする要素がいくつかある.私はこれらの要素を切り捨てた形で基礎を学んだ 上で,さらにこれらの要素が入ることでどのような影響が生じるかを考えた方が 良いと考える(しかし本テキストではそこまではしていない).したがって本テ キストで得た知識を鵜呑みにして拡大解釈するのは危険だ.このテキストは知識 を提供するものではなく,「考え方」を提供するものと思ってほしい.拡大解釈 の危険性については,本テキストの最後でもう一度述べたいと思う.
※本ページは前述の「 ふるかわ通信板」に投稿した内容を東北大学医学部附属病院の 佐藤 大氏が 自発的にまとめて下さったものです.佐藤氏には非常に感謝しています.
方針に従って,まずは1次元の錐体応答空間の場合について考えてみる. つまり錐体を1種類(ここではM錐体としておこう)しか持たない場合だ.
M錐体の波長感度特性をピーク1つ持つシンプルな山型 と仮定しよう.

図 1-1 理想化した錐体Mの波長感度特性
図 1-1 の意味だが,光強度を一定にして波長だけを変えた時, どのような応答振幅を示すかをグラフにしたものだ.つまり波長Cの光に対しては, 波長BやDの光の倍の応答振幅を示すということだ(光強度が同じならば).
ついでに錐体の特性は線形で,光強度(明るさ)を2倍3倍にすると応答振幅も 2倍3倍になると仮定しておこう.
さてこの場合,網膜から得られる応答は (m ) という1次元ベクトル, つまりスカラー量で表わされる(m はM錐体の応答振幅).
さらに話を簡単にするため,当分の間,単波長光のみを扱うことにする. 単波長光というのは読んで字の如く,単一の波長しか含まない光のことだ. 現実の世界で単波長光にお目にかかることはあまりなく, せいぜいプリズムで分解したときくらいしか見ない. しかし複数の波長成分を含んだ光刺激や,連続スペクトルの光刺激に対する 応答を考えるのはとてもやっかいなので,まずは単波長光で考える.
さて,波長をいろいろ変え(図 1-1 の 波長A〜E),また光強度もいろいろ変え(1, 2, 3, 4倍としてみた. 線形なので単位は適当)たときの光応答が (m ) 空間でどこにプロットされるか を示したのが図 1-2 だ. (波長A〜Eは色分けして示した.これはあくまでも区別するための色で, そのように見えて感じるわけではない).
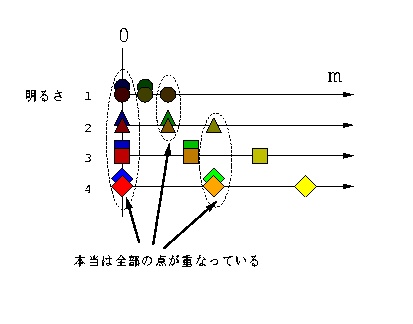
図 1-2 単波長光の強度(明るさ)と波長を変えた時に生じる錐体Mの応答の大きさ.
そもそもスカラー量でしか感じられないのだから,1次元の錐体応答空間では 光の強度と波長を区別することはできない.(m ) 空間上の1点は さまざまな光強度・波長の光に対応するため,元々の光強度と波長の情報を 復元できないと言ってもいい.したがってこのような生物にとって,光刺激は 明るく感じるか暗く感じるかだけで,それ以上の区別はない. ヒトならば図 1-3 の上段のように 感じるところだろうが,下段のように感じるに違いない.
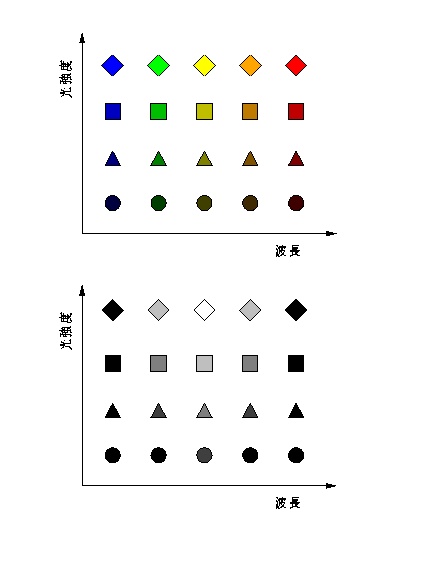
図 1-3 M錐体を持つ生物による色の知覚.上段がヒト.
Next: 2次元の場合
[ テキスト版 ]
[ 色覚テキスト Top ]