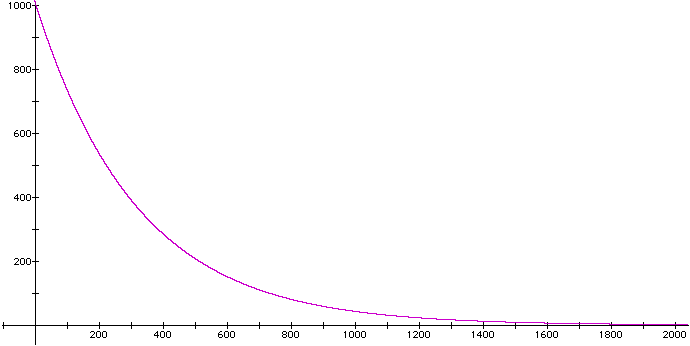
図1 ハマり率グラフ(y = 1000(316/317)^x)
最近結構パチンコに行くんですが,冷静に考えてパチンコって勝てるもんなんだろうか? 勝てるとしたら具体的にどう言う条件を満たせば良いのか? 。。。などの疑問が浮かんで来たので,いろいろ計算するついでにここにまとめておきます。
ここでは(少なくとも最近よく行く店では普通な)5 & 15 の CR で,大当たり確率 1/317(確変時 1/67),確変突入率 1/2,大当たり一回あたりの出玉 2100 発,というスペックの機種について考えていきますが,ここに出て来た単語が良く分からんという人は「知らない人用パチンコ解説」を最初に読んで下さい。
「素直に」解釈した場合のパチンコのアルゴリズムは次のようようなもので,それぞれの次の段階に進むかどうかは確率的事象と解釈されます。
このうち「リーチがかかる」以降については,その機種のプログラムによって決まっていると考えられます。例えば数字が回転すると 20 回に 1 回はリーチがかかり,そのうち千回に 1 回は大当たり。そうでないうちの 3 回に 1 回はスーパーリーチに発展し,その 10 回に 1 回は大当たりでそうでない場合の 5 回に 1 回はさらに発展,すると さらにそのうち 3 回に 1 回は大当たり。それぞれの大当たりのうち 2 回に 1 回は確変。。。などという感じになっています。
しかしパチンコ雑誌などの記事を見る限り,実際のパチンコのプログラムはこういう見た目通りには書かれていないようです。プログラム内部に 0.3 秒とかで一周するルーレットがあります。このルーレットは,例えば 634 マスあって,このうち一つが大当たり,他の一つが確変大当たり,という具合になってます。スタートチャッカーに玉が入った瞬間にこのルーレットが指していたマスによって,外れか大当たりか確変大当たりかが決まります。そして大当たりの場合にどのリーチを見せるかを適当に割振ります。また外れの場合にも一定の確率でリーチを見せるようにします。この際にリーチの信頼率が低ければ低いほど,外れた時に見せる量を増やします。リーチを見せない場合には,2つめに止まる数字を1つめの数字以外から適当に選びます。
したがってリーチアクションを気にしなければ,当たりか外れかは画面が動く前に決定済みだということになります。このようなプログラムで当たりが決定される場合には,たまに見かける「特定の数字の並びが出ると大当たりが近い」とか「リーチが良く出るのでもうすぐ当たる」というのは単なる迷信だということになります。
上記の当たり決定アルゴリズムが使われているとすれば,当たる確率や勝つ確率を計算するにはリーチ予告やリーチアクションの有無は一切関係ない事になります。この前提のもとで,いろいろと計算してみます。
さて,当たった時にはとりあえず一回分の出玉は保証されますが,実際には連荘して一杯出て来たぞ,なんつー事もあります。平均すると何発くらいの出玉が期待されるんでしょうか?
とりあえずは連荘回数を計算してみましょう。最近では平均的な確変突入率 1/2 の機種の場合だと,1回で終わる(確変を引けない)可能性が 1/2,2回目で終わる可能性が (1/2)^2,3回目で終わる可能性が (1/2)^3。。。となります。で,n 回目で終わる可能性は (1/2)^n なので,何連荘するかという期待値は
1/2 + 2(1/2)^2 + 3(1/2)^3 + ... + n(1/2)^n
となります。1 + a + a^2 + a^3 ... = 1/(1 - a) という極限操作を利用してこれを計算する(でも省略)と,一般解として n/(1-n)^2 という式が得られます。したがって確変突入率が 1/2(つまり n = 2)の場合には,この期待値として 2 という結果が得られます。つまり当たれば平均2連荘するという訳です。
最近の機種では大当たり一回での出玉は 2100 発とかが普通のようなので,次に当たりが出た時に出てくる玉の数の期待値は
2 x 2100 発 - 確変で消費した玉数
ということになります。
ひどい時だと 1500 回とか回ってるのにまだ出ない!なんてこともありますが,計算上どれくらいの確率で起こるんでしょうか?
この計算は簡単で,当たり確率 1/317 の機種であれば外れ率(= 316/317)の n 乗で n 回まで回る確率が分かります。ある台で打ち始めるというのを 1000 回やった場合,x 回まで当たらない確率を計算してグラフで表示しました。これを見ると 1000 回のうちの 500 回は 220 回転までに当たるという事になります。また 1000 回のうち 200 回ちょっとは 500 回転以上,42 回は 1000 回転以上,9 回弱は 1500 回転以上ハマり,2000 回以上ハマる確率は 1000 回のうち 1.8 回ということになります。

図1 ハマり率グラフ(y = 1000(316/317)^x)
いろいろ計算しましたが,これを平均すると,当たるまでの回転数の期待値は単純に 317 回転という値が得られます。
確変引いたのにいつになっても当たらなーい。。。なんて事もたまにあります。ついこないだも確変突入してから 255 回も回しました。(^^;; ということで,前項の確変バージョンです。
当然ですが,確変モードの時の方が収束ははるかに早くなっています。確変の時には 1000 回のうちの 500 回は 46 回転までに当たる計算になります。また 1000 回のうちの 222 回は 100 回転以上,50 回弱は 200 回転以上,11 回ほどは 300 回転以上ハマり,400 回転以上ハマるのは,1000 回のうち 2.4 回ほどという計算されます。
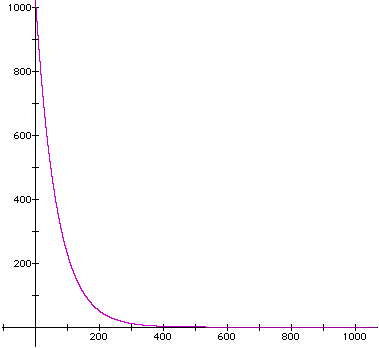
図2 ハマり率グラフ(y = 1000(66/67)^x)
これもまた,当たるまでの回転数の期待値は単純に 67 回となります。
打ち出した玉 x 発に 1 発の割合いでスタートチャッカーに入るとします。そしてスタートチャッカーに玉が入るたびに 5 発の玉が出てくるとします。このときに 500 円分(つまり 125 発)の手持ち玉を打ち始めてなくなるまでに,何回転するのかを計算します。
まず 125 発を打った時点でスタートチャッカーに入る玉の数は 125/x です。そしてその結果として 5 発ずつ出てくるので 5 * 125/x 個の玉が手元に残っています。この分の玉を打つと (5 * 125/x)/x = (5/x) * (125/x) 個がチャッカーに入ります。さらにここで 5 発ずつ出て来た 5 * (5 * 125/x)/x 個の玉を打つと 5 * (5 * 125/x)/(x * x) = (5/x)^2 * (125/x) 個がチャッカーに入ります。これを整理すると
(125/x) * (1 + (5/x) + (5/x)^2 + (5/x)^3 + ... = (125/x) * (1/(1 - (5/x)))
という式が得られます。たとえば 10 発に 1 発の割合いでチャッカーに入るとすると,500 円で (125/10) * (1/(1 - (5/10))) = 25 回転するという計算になります。そんなに回る台はなかなかないだろうけど。(^^;;;
さて,前章の確率論をもとに,どういう条件を満たすと玉数が増えると期待できるのか,考えてみます。
スペックは,5 & 15 の CR で,大当たり確率 1/317(確変時 1/67),確変突入率 1/2,大当たり一回あたりの出玉 2100 発という想定です。この時に連荘回数の期待値は 2 回です。確変中はスタートチャッカーのチューリップが頻繁に開くので,出玉はそれほど減りません。機種によっては上手く打つと増やす事も出来ます。ということで,ここでは確変中には玉数は増えも減りもしないとして計算します。
連荘回数の期待値は 2 回で,大当たり 1 回あたりの出玉は 2100 発です。したがって一度の大当たりで 4200 発の出玉が期待されます。そして大当たりが出るまでの回転数の期待値は 317 回転なので,4200 発打って 317 回以上スタートチャッカーに入れば,玉数の増加が期待できます。ただしこれは,すでに手元に玉がある,すなわち一度当たったあとの話ですな。(^^;;
さて,やっと「経済学」っぽい話になります。(^^;; ここからは店に依存する条件がいろいろ出て来ます。とりあえずは仙台で良くあるパターンで説明します。
まず支出部分,すなわち貸玉ですが,一発4円で借りられるのが普通です。次に収入部分です。仙台では 1 発 2.5 円の店が多いので,以下では 2.5 円換算の場合を例にとって話を進めます。
以上のように玉を借りる時と換金する時のレートが違うので,単に玉が増えたからと言って得をするとは限りません。例えば 1000 円で 250 発の玉を借りて,これが 300 発に増えても 750 円分の特殊景品としか交換できないので,損をすることになります。
これを考慮すると次のように計算できます。大当たり一回あたり 4200 発の出玉が期待できるということは 4200 x 2.5 円 = 約 10000 円の収入が大当たり一回で得られる事になります。そして大当たりは 317 回転に 1 回の割合なので,10000 円で 317 回転以上まわるなら,確率的に黒字になります。317 x ( 500 / 10000 ) = 15.85 なので,平均して 500 円で 16 回以上回る台ならば黒字,ということになります。10000 円分の貸玉は 2500 発なので 7.9 発に 1 発の割でスタートチャッカーに入る計算になりそうですが,実際には 1 発入るたびに 5 発玉が出てくるので,その分修正する必要があります。先ほどの式を使うと約 12.8 発に 1 発がスタートチャッカーに入れば良いという結果になります。
以上の計算は借りた玉だけで打ち続けた場合です。一度当たって出て来た玉で打つ場合には,4200 発で 317 回まわせば良いという事になるので,単純に割算すると 13.2 発に 1 発がスタートチャッカーに入れば良いという事になります。出玉分を修正すると,18.25 発に 1 発がチャッカーに入れば黒字が期待できるという結果になります。借りた玉だけで打つ場合と比べると,チャッカーに入る確率が 3 割ほど低くても大丈夫だという結果です。
ちなみに等価交換の店の場合には,4200 x 4 円 = 約 16,000 円の収入が大当たり一回で得られます。4200 発で 317 回転ということは,前述の通り 18.25 発に 1 発がチャッカーに入れば黒字が期待できます。前述の式を使うと
x = 18.25
y = (125/x) * (1/(1 - (5/x)))
∴ x = 9.4
となって,500 円(125 発)で 9.4 回転以上まわる台なら黒字が期待できることになります。